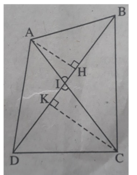
Giả sử hai đường chéo AC, BD cắt nhau tại I, ∠ (AIB) = α là góc nhọn (xem h.bs.9)
Kẻ đường cao AH của tam giác ABD và đường cao CK của tam giác CBD.
Ta có: AH = AI.sin α , CK = CI.sin α
Diện tích tam giác ABD là S A B D = 1/2 BD.AH.
Diện tích tam giác CBD là S C B D = 1/2 BD.CK.
Từ đó diện tích S của tứ giác ABCD là:
S = S A B D + S C B D = 1/2BD.(AH + CK)
= 1/2 BD.(AI + CI)sin α = 1/2BD.AC.sin α











