Question

Chứng minh:

a, Diện tích của một tam giác bằng nửa tích của hai cạnh nhân với sin của góc nhọn tạo bởi các đường thẳng chứa hai cạnh ấy

b, Diện tích của tứ giác bất kỳ bằng nửa tích của hai đường chéo nhân với sin của góc nhọn tạo bởi hai đường chéo

Answer 1

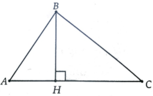
a, Giả sử tam giác ABC có  A ^ < 90 0  kẻ đường cáo BH. Ta có BH=AB.sin A ^

=>  S ∆ A B C = 1 2 A C . B H =  1 2 A B . A C . sin A

b, Giả sử tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O có  A O B ^ = α < 90 0 . Kẻ AH ⊥ BD, tại H và CK ⊥ BD tại K

Ta có: AH = OA.sinα

=>  S A B D = 1 2 B D . A H =  1 2 B D . O A . sin α

Tương tự:  S C B D = 1 2 B D . C K =  1 2 B D . O C . sin α

=>  S A B C D = S A B D + S C B D =  1 2 B D . O A . sin α +  1 2 B D . O C . sin α =  1 2 B D . A C . sin α