Chọn B.
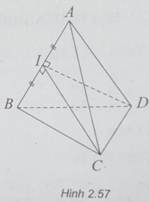
(h.2.57) Gọi I là trung điểm AB. Dễ thấy IC = ID. Khi quay tứ diện quanh AB, ta có hai hình nón: Hình nón đỉnh A, đáy là hình tròn tâm I, bán kính IC; Hình nón đỉnh B, đáy là hình tròn tâm I, bán kính IC.
Chọn B.

(h.2.57) Gọi I là trung điểm AB. Dễ thấy IC = ID. Khi quay tứ diện quanh AB, ta có hai hình nón: Hình nón đỉnh A, đáy là hình tròn tâm I, bán kính IC; Hình nón đỉnh B, đáy là hình tròn tâm I, bán kính IC.
Cho tứ diện ABCD có AD ⊥ (ABC) và BD ⊥ BC. Khi quay tứ diện đó xung quanh trục là cạnh AB, có bao nhiêu hình nón được tạo thành?
A. Một B. Hai
C. Ba D. Bốn
Cho tứ diện đều ABCDABCD. Khi quay tứ diện đó quanh trục ABAB có bao nhiêu hình nón khác nhau được tạo thành?
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (DBC) và D B C ^ = 90 ° . Khi quay các cạnh của tứ diện xung quanh trục là cạnh AB, có bao nhiêu hình nón được tạo thành?
![]()
![]()
![]()
![]()
Cho tứ diện ABCD có AD ⊥ (ABC) và BD ⊥ BC. Khi quay tất cả các cạnh của tứ diện đó quanh cạnh AB có những hình nón nào được tạo thành ? Hãy kể tên các hình nón đó.
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC) và cạnh BD vuông góc với cạnh BC. Biết AB = AD = a. Tính diện tích xung quanh của hình nón và thể tích của khối nón được tạo thành khi quay đường gấp khúc BDA quanh cạnh AB.
Cho tam giác ABC vuông cân tại A, AB=a, cho quay quanh trục BA tạo thành hình nón tròn xoay. Tính diện tích xung quanh S x q của hình nón đó
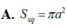
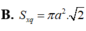
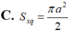
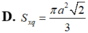
Một tứ diện đều cạnh a có một đỉnh trùng với đỉnh hình nón, ba đỉnh còn lại nằm trên đường tròn đáy của hình nón. Khi đó diện tích xung quanh của hình nón bằng:
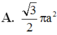
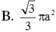
![]()
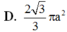
Một hình chữ nhật ABCD có AB = a và B A C ^ = α với 0 ∘ < α < 90 ∘ . Cho hình chữ nhật đó quay quanh cạnh AB, tam giác ABC tạo thành một hình nón có diện tích xung quanh là S. Mệnh đề nào là sai?
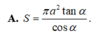
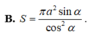
![]()
![]()
Một hình tứ diện đều cạnh a có một đỉnh trùng với đỉnh của hình nón tròn xoay còn ba đỉnh còn lại của tứ diện nằm trên đường tròn đáy của hình nón. Diện tích xung quanh của hình nón tròn xoay là:
A. 1 3 πa 2 3 B. πa 2 2
C. 1 3 πa 2 2 D. 1 2 πa 2 3