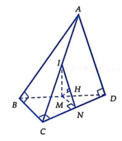
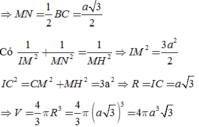Các câu hỏi tương tự
Cho khối trụ có bán kính đáy bằng a và thiết diện đi qua là một hình vuông. Thể tích khối trụ là:A. 2
π
a
3
B. 2
π
a
3
/3C. 4
π
a
3
D.
π
a
3
Đọc tiếp
Cho khối trụ có bán kính đáy bằng a và thiết diện đi qua là một hình vuông. Thể tích khối trụ là:
A. 2 π a 3 B. 2 π a 3 /3
C. 4 π a 3 D. π a 3
Một hình nón có đường kính đáy là 2a
π
3, góc ở đỉnh 120
°
. Thể tích của khối nón đó theo a là:A. 2
3
π
a
3
B. 3
π
a
3
C.
π
a
3
D.
π...
Đọc tiếp
Một hình nón có đường kính đáy là 2a π 3, góc ở đỉnh 120 ° . Thể tích của khối nón đó theo a là:
A. 2 3 π a 3 B. 3 π a 3
C. π a 3 D. π a 3 3
Cho hình lập phương ABCD.ABCD. Gọi (H) là hình cầu nội tiếp hình lập phương đó. Khi đó:
V
H
V
ABCD
.
A
B
C
D
A....
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D'. Gọi (H) là hình cầu nội tiếp hình lập phương đó. Khi đó:
V H V ABCD . A ' B ' C ' D '
A. π /6 B. π /4
C. π /3 D. π /( 3 )
Cho hình lập phương ABCD.ABCD. Gọi (H) là hình trụ tròn xoay ngoại tiếp hình lập phương đó. Khi đó:
V
H
V
ABCD
.
A
B
C
D...
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D'. Gọi (H) là hình trụ tròn xoay ngoại tiếp hình lập phương đó. Khi đó: V H V ABCD . A ' B ' C ' D '
A. 3/2 B. π /2
C. π /3 D. π /( 3 )
Diện tích xung quanh của hình trụ có bán kính đáy a và đường cao a
3
là:A. 2
π
a
2
3
B. 2
π
a
2
C.
π
a
2
D.
π
a...
Đọc tiếp
Diện tích xung quanh của hình trụ có bán kính đáy a và đường cao a 3 là:
A. 2 π a 2 3 B. 2 π a 2
C. π a 2 D. π a 2 3
Cho hình lập phương ABCD.ABCD. Gọi (H) là hình nón tròn xoay nội tiếp hình lập phương đó. Khi đó:
V
H
V
ABCD
.
A
B
C
D...
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D'. Gọi (H) là hình nón tròn xoay nội tiếp hình lập phương đó. Khi đó: V H V ABCD . A ' B ' C ' D '
A. 1/3 B. π /6
C. π /8 D. π /12
Cho hình chóp S.ABC đáy ABC là tam giác vuông tại C, có cạnh AB a = , cạnh bên SA vuông góc mặt phẳng đáy và SA a = 3 . Tính thể tích V khối cầu ngoại tiếp hình chóp.
A. V= 2 2 3 3 a .
B. V= 3 4a .
C. V= 32 3 3 πa .
D. V= 4 3 3 πa .
Quay hình phẳng G giới hạn bởi các đường: y = x 3 ; y = 1, x = 0 xung quanh trục Oy. Khi đó thể tích của khối tròn xoay này bằng:
A. π B. 5 π /3
C. 3 π /5 D. 3/5
Một hình hộp chữ nhật có ba kích thước lần lượt là a, b, c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Diện tích của mặt cầu (S) theo a, b, c là:A.
π
(
a
2
+
b
2
+
c
2
) B. 2
π
(
a...
Đọc tiếp
Một hình hộp chữ nhật có ba kích thước lần lượt là a, b, c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Diện tích của mặt cầu (S) theo a, b, c là:
A. π ( a 2 + b 2 + c 2 ) B. 2 π ( a 2 + b 2 + c 2 )
C. 4 π ( a 2 + b 2 + c 2 ) D. π /2.( a 2 + b 2 + c 2 )