Các câu hỏi tương tự
Cho
△
A
B
C
có A(0;2), B(4;0), C(1;1), và G là trọng tâm. Điểm M thuộc đường thẳng y2 sao cho
M
A
→
+
M
B...
Đọc tiếp
Cho △ A B C có A(0;2), B(4;0), C(1;1), và G là trọng tâm. Điểm M thuộc đường thẳng y=2 sao cho M A → + M B → + M C → nhỏ nhất, khi đó tọa độ M G → là
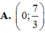
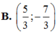
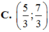
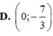
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD, M là điểm thuộc cạnh BC sao cho MB 2MC. Mệnh đề nào sau đây đúng? A.
M
G
∥
(
B
C
D
)
B.
M
G
∥
(
A
C
D
)
C.
M
G
∥
(
A...
Đọc tiếp
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD, M là điểm thuộc cạnh BC sao cho MB = 2MC. Mệnh đề nào sau đây đúng?
A. M G ∥ ( B C D )
B. M G ∥ ( A C D )
C. M G ∥ ( A B D )
D. M G ∥ ( A B C )
Cho tứ diện ABCD, G là trọng tâm của tam giác ABD, M là điểm trên cạnh BC sao cho MB = 2MC. Khẳng định nào sau đây là đúng?
A. MG // (ACD)
B. MG // (ABC)
C. MG // AB
D. MG cắt AC
Cho tứ diện ABCD, G là trọng tâm tam giác ABD, N là trung điểm của AD, M là trung điểm trên cạnh BC sao cho MB = 2MC. Khẳng định nào sau đây là đúng?
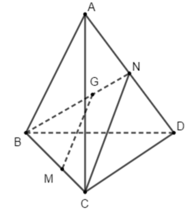
A. MG // CN
B. MG và CN cắt nhau
C. MG // AB
D. MG và CN chéo nhau.
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD. M là điểm trên cạnh BC sao cho MB=2MC. Khi đó đường thẳng MG song song với mặt phẳng nào dưới đây?
A. (ACD)
B. (BCD)
C. (ABD)
D. (ABC)
Cho tứ diện ABCD. Tìm vị trí điểm M trong không gian sao cho:
M A 2 + M B 2 + M C 2 + M D 2 đạt giá trị cực tiểu.
Cho hình bình hành ABCD. Tập hợp các điểm M thỏa mãn
M
A
→
+
M
B
→
-
M
C
→
M
D
→
A. một đường tròn. B. một đường thẳng. C. tập rỗng. D. một đoạn thẳng...
Đọc tiếp
Cho hình bình hành ABCD. Tập hợp các điểm M thỏa mãn M A → + M B → - M C → = M D →
A. một đường tròn.
B. một đường thẳng.
C. tập rỗng.
D. một đoạn thẳng.
cho A(0;6), B(2;5). Tìm trên (d): x-2y+2=0 điểm M sao cho
a) MA+MB có giá trị nhỏ nhất
b) I MA -MB I có giá trị lớn nhất.
Cho tứ diện ABCD có G là trọng tâm tam giác ABC. Gọi M là trung điểm AB P, là điểm nằm trên đoạn AD sao cho MP không song song BD. Giao tuyến của ( ) MPG và ( ) BCD là




