Các câu hỏi tương tự
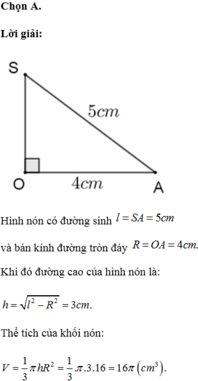
Cho tam giác SOA vuông tại O có OA4cm, SA5cm, quay tam giác SOA xung quanh cạnh SO được hình nón. Thể tích của khối nón tương ứng là
Đọc tiếp
Cho tam giác SOA vuông tại O có OA=4cm, SA=5cm, quay tam giác SOA xung quanh cạnh SO được hình nón. Thể tích của khối nón tương ứng là
![]()
![]()
![]()
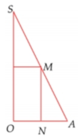
Cho tam giác SOA vuông tại O, có MN//SO với M, N lần lượt nằm trên cạnh SA,OA như hình vẽ bên. Đặt SOh không đổi. Khi quay hình vẽ quanh SO thì tạo thành một hình trụ nội tiếp hình nón đỉnh S có đáy là hình tròn tâm O, bán kính ROA. Tìm độ dài của MN theo h để thể tích khối trụ là lớn nhất.
Đọc tiếp
Cho tam giác SOA vuông tại O, có MN//SO với M, N lần lượt nằm trên cạnh SA,OA như hình vẽ bên. Đặt SO=h không đổi. Khi quay hình vẽ quanh SO thì tạo thành một hình trụ nội tiếp hình nón đỉnh S có đáy là hình tròn tâm O, bán kính R=OA. Tìm độ dài của MN theo h để thể tích khối trụ là lớn nhất.
![]()
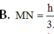
![]()
![]()
Cho tam giác ABC vuông tại A, cạnh AB4, BC5. Quay tam giác ABC quanh AB được khối nón có thể tích
V
1
, quay tam giác ABC quanh AC được khối nón có thể tích
V
2
thì A.
V
1
V
2
12
π
B.
V
1
V
2
C. ...
Đọc tiếp
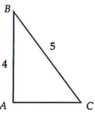
Cho tam giác ABC vuông tại A, cạnh AB=4, BC=5. Quay tam giác ABC quanh AB được khối nón có thể tích V 1 , quay tam giác ABC quanh AC được khối nón có thể tích V 2 thì
A. V 1 = V 2 = 12 π
B. V 1 > V 2
C. V 1 = V 2 = 16 π
D. V 1 < V 2
Cắt hình nón đỉnh S bởi mặt phẳng đi qua trục ta được một tam giác vuông cân có cạnh huyền bằng a √2
Tính diện tích xung quanh, diện tích đáy và thể tích của khối nón tương ứng.
Trong không gian, cho tam giác OAB vuông tại O có OA 4a, OB 3a. Nếu cho tam giác OAB quay quanh cạnh OA thì mặt nón tạo thành có diện tích xung quanh
S
x
q
bằng bao nhiêu? A.
S
x
q
9
πa...
Đọc tiếp
Trong không gian, cho tam giác OAB vuông tại O có OA = 4a, OB = 3a. Nếu cho tam giác OAB quay quanh cạnh OA thì mặt nón tạo thành có diện tích xung quanh S x q bằng bao nhiêu?
A. S x q = 9 πa 2
B. S x q = 16 πa 2
C. S x q = 15 πa 2
D. S x q = 12 πa 2
Trong không gian cho tam giác ABC vuông tại A có ABa và BC2a. Quay tam giác ABC xung quanh cạnh AB ta thu được khối nón có thể tích bằng A.
π
a
3
.
B.
3
π
a
3
.
C.
3
3
π
a
3
.
D.
2
3
π
a...
Đọc tiếp
Trong không gian cho tam giác ABC vuông tại A có AB=a và BC=2a. Quay tam giác ABC xung quanh cạnh AB ta thu được khối nón có thể tích bằng
A. π a 3 .
B. 3 π a 3 .
C. 3 3 π a 3 .
D. 2 3 π a 3 .
Cho tam giác ABC vuông tại A. ABc, ACb. Quay tam giác ABC xung quanh đường thẳng chứa cạnh AB được một hình nón có thể tích bằng:
Đọc tiếp
Cho tam giác ABC vuông tại A. AB=c, AC=b. Quay tam giác ABC xung quanh đường thẳng chứa cạnh AB được một hình nón có thể tích bằng:
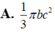
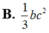
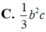
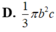
Cho tam giác ABC vuông tại A và có AB4, AC5. Tính thể tích của khối nón sinh ra khi tam giác ABC quay xung quanh cạnh AB
Đọc tiếp
Cho tam giác ABC vuông tại A và có AB=4, AC=5. Tính thể tích của khối nón sinh ra khi tam giác ABC quay xung quanh cạnh AB
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy
S
C
a
6
. Khi tam giác SAC quay quanh cạnh SA thì đường gấp khúc SAC tạo thành một hình nón tròn xoay. Thể tích của khối nón tròn xoay đó là: A.
4
πa
3
3
B.
a
3
π...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy S C = a 6 . Khi tam giác SAC quay quanh cạnh SA thì đường gấp khúc SAC tạo thành một hình nón tròn xoay. Thể tích của khối nón tròn xoay đó là:
A. 4 πa 3 3
B. a 3 π 2 6
C. πa 3 3 3
D. πa 3 3 6