Đáp án A
Theo bài ra , ta có khối nón tạo thành có chiều cao h = S O = 4 c m và có bán kính đáy r = O A = 3 c m Vậy thể tích khối nón cần tính là V = 1 3 π r 2 h = π 3 .3 2 .4 = 12 π c m 3
Đáp án A
Theo bài ra , ta có khối nón tạo thành có chiều cao h = S O = 4 c m và có bán kính đáy r = O A = 3 c m Vậy thể tích khối nón cần tính là V = 1 3 π r 2 h = π 3 .3 2 .4 = 12 π c m 3
Cho tam giác SOA vuông tại O có OA = 4cm, SA = 5cm, quay tam giác SOA xung quanh cạnh SO được hình nón. Thể tích của khối nón tương ứng là:
A. 16 π ( cm 3 )
B. 15 π ( cm 3 )
C. 80 π 3 ( c m 3 )
D. 36 π ( cm 3 )
Cho tam giác SOA vuông tại O, có MN//SO với M, N lần lượt nằm trên cạnh SA,OA như hình vẽ bên. Đặt SO = h không đổi. Khi quay hình vẽ quanh SO thì tạo thành một hình trụ nội tiếp hình nón đỉnh S có đáy là hình tròn tâm O, bán kính R = OA. Tìm độ dài của MN theo h để thể tích khối trụ là lớn nhất
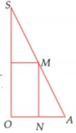
A. MN = h/2
B. MN = h/3
C. MN = h/4
D. MN = h/6
Cho tam giác SOA vuông tại O có MN//SO với M, N lần lượt nằm trên cạnh SA, OA như hình vẽ bên dưới. Đặt S O = h không đổi. Khi quay hình vẽ quanh SO thì tạo thành một hình trụ nội tiếp hình nón đỉnh S có đáy là hình tròn tâm O bán kính R = O A . Tìm độ dài của MN theo h để thể tích khối trụ là lớn nhất.
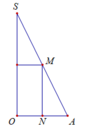
A. M N = h 3
B. M N = h 4
C. M N = h 6
D. M N = h 2
Cho tam giác SOA vuông tại O có MN//SO với M, N lần lượt nằm trên cạnh SA, OA như hình vẽ bên. Đặt SO = h không đổi. Khi quay hình vẽ quanh SO thì tạo thành một hình trụ nội tiếp hình nón đỉnh S có đáy là hình tròn tâm O bán kính R = OA. Tìm độ dài của MN theo h để thể tích khối trụ là lớn nhất
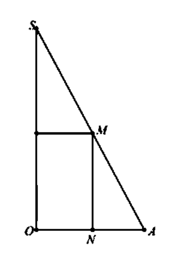
A. M N = h 2
B. M N = h 3
C. M N = h 4
D. M N = h 6
Cho tam giác ABC vuông tại A. AB=c,AC=b. Quay tam giác ABC xung quanh đường thẳng chứa cạnh AB được một hình nón có thể tích bằng
A. 1 3 πbc 2
B. 1 3 b c 2
C. 1 3 b 2 c
D. 1 3 πb 2 c
Cho tam giác ABC cân tại A, có cạnh A B = a 5 , B C = 2 a . Gọi M là trung điểm của BC. Khi tam giác quay quanh trục MA ta được một hình nón và khối nón tạo bởi hình nón đó có thể tích là
A. V = 5 3 π a 2
B. V = 2 π a 3
C. V = 2 3 π a 3
D. V = 4 3 π a 3
Cho ∆ A B C vuông tại A có AB = 3; AC = 4. Quay tam giác quanh AB ta được hình nón tròn xoay có diện tích xung quanh S 1 và quay tam giác quanh AC ta thu được hình nón xoay có diện tích xung quanh S 2 . Tính tỉ số S 1 S 2
A. 4 3
B. 3 4
C. 4 5
D. 3 5
Cho hình nón có thể tích bằng 12 π và diện tích xung quanh bằng 15. Tính bán kính đáy của hình nón biết bán kính là số nguyên dương.
A. 4
B. 3.
C. 6
D. 5
Cho tam giác ABC vuông tại A. Các cạnh AB, AC, BC của hình tam giác lần lượt là 3; 4; 5. Tính thể tích hình nón khi quay tam giác quanh trục AB
A. 12 π
B. 16 π
C. 48 π
D. Đ á p á n k h á c