Xét ΔMNQ có:
`MN^2 + MQ^2 = NQ^2`
=> ΔMNQ vuông tại M
=> M thuộc đường tròn đường kính NQ (đpcm)
Đúng 1
Bình luận (2)
Các câu hỏi tương tự
Cho tam giác MNQ vuông tại M có MNMQ và MNQ60 độME là phân giác của góc NMQ (E thuộc NQ)Vẽ đường thẳng qua E và vuông góc với đường thẳng NQ cắt MQ tại H, cắt đường thẳng MN tại F. Gọi O là tâm đường tròn ngoại tiếp tam giác NFQ.a) C/M: Tứ giác FMEQ nội tiếp trong một đường tròn. Xác định vị trí tâm I của đường tròn đó.b) C/M: OE//NHgiúp mình với ạ. Các bạn vẽ hình cho mình với nhé
Đọc tiếp
Cho tam giác MNQ vuông tại M có MN<MQ và MNQ=60 độ
ME là phân giác của góc NMQ (E thuộc NQ)
Vẽ đường thẳng qua E và vuông góc với đường thẳng NQ cắt MQ tại H, cắt đường thẳng MN tại F. Gọi O là tâm đường tròn ngoại tiếp tam giác NFQ.
a) C/M: Tứ giác FMEQ nội tiếp trong một đường tròn. Xác định vị trí tâm I của đường tròn đó.
b) C/M: OE//NH
giúp mình với ạ. Các bạn vẽ hình cho mình với nhé
1 tháng 4 2022 lúc 21:18
Cho tứ giác MNPQ nội tiếp đường tròn đường kính MQ. Hai đường chéo MP và NQ cắt nhau tại E. Gọi F là điểm thuộc đường thẳng MQ sao cho EF vuông góc với MQ. Đường thẳng PF cắt đường tròn đường kính MQ tại điểm thứ 2 là K. Gọi L là giao điểm của NQ và PF. Chứng minh rằng: NQ.LE = NE.LQ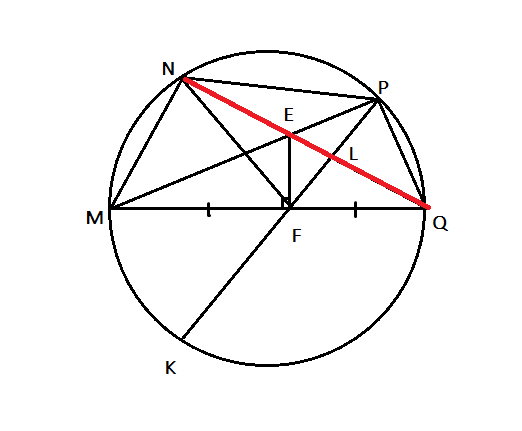
1. Cho hình trụ có diện tích xung quanh 72pi, biết chiều cao lớn hơn bán kính đường tròn đấy là 6cm. Tính V.
2. Cho hình nón có chu vi đáy 18pi. Độ dài đường sinh lớn hơn bán kính 6cm. Tính V.
3. Cho tam giác MNQ vuông tại Q MQ=12cm, NQ=16cm. Tính diện tích xung quanh của hình tạo thành khi quay tam giác MNQ một vòng quanh cạnh MN.
cho tam giác MNP vuông tại M. Trên MN lấy một điểm Q, vẽ đường tròn đường kính NQ và cắt NP tại E. kế đường thẳng PQ cắt đường tròn tại D
a/ Vẽ hình
b/ Chứng minh : tứ giác MPND nội tiếp
c/ Chứng minh : góc DMN = goc DPN
d/ Chứng minh : MN là đường phân giác của góc DME
Bài 5 (1 điểm): Cho tam giác MNP vuông tại M, có MN = 6 cm, MP = 8 cm. Chứng minh rằng các
đỉnh M, N, P cùng thuộc một đường tròn. Hãy xác định tâm và tính độ dài bán kính của đường tròn
đó.
Cho tam giác ABC nhọn có AB < AC, đường cao AD. Đường tròn tâm ),đường kính BC. Vẽ AM và AN là hai tiếp tuyến của đường tròn.
a. Chứng minh 5 điểm M, N, O, D. A cùng thuộc một đường tròn
b. Gọi MN cắt AD tại H. Chứng minh H là trực tâm tam giác ABC
Cho tam giác MNQ(MN< MQ) nhọn, có các đường cao MD, NE, QF và trực tâm H. nội tiếp (O)
a> Chứng Minh:các tứ giác NFHD và NFED nội tiếp?
b> Chứng Minh: H là tâm đường tròn nội tiếp tam giác DFE
Câu 5. (3,5 điểm) Cho tam giác ABC (AB AC) có ba góc nhọn nội tiếp trong đường tròntâm O, bán kính R. Gọi H là giao điểm của ba đường cao AD, BE, CF của tam giác ABC.a) Chứng minh rằng 4 điểm A, E, H, F cùng thuộc một đường trònb) Vẽ đường kính AK của đường tròn (O). Chứng minh tam giác ABD và tam giác AKCđồng dạng với nhau. Suy ra AB.AC 2R.AD.c) Chứng minh rằng OC vuông góc với DE
Đọc tiếp
Câu 5. (3,5 điểm) Cho tam giác ABC (AB < AC) có ba góc nhọn nội tiếp trong đường tròn
tâm O, bán kính R. Gọi H là giao điểm của ba đường cao AD, BE, CF của tam giác ABC.
a) Chứng minh rằng 4 điểm A, E, H, F cùng thuộc một đường tròn
b) Vẽ đường kính AK của đường tròn (O). Chứng minh tam giác ABD và tam giác AKC
đồng dạng với nhau. Suy ra AB.AC = 2R.AD.
c) Chứng minh rằng OC vuông góc với DE
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài MN của hai đường tròn (M ∈ (O), N ∈ (O’)). Gọi P là điểm đối xứng với M qua OO’, Q là điểm đối xứng với N qua OO’. Chứng minh rằng: MN + PQ = MP + NQ.
1. Cho tam giác ABC nội tiếp đương tròn O. Đường cao AD cắt đường tròn tại E, vẽ đường kính AM.a. Chứng minh rằng: BEMC là hình thang cânb. Chứng minh rằng: DA2 + DB2 + DE2 + DC2 4.R22. Cho tam giác ABC đều, đường cao AH, điểm M thuộc BC. Gọi P và Q là hình chiếu của M trên AB, AC.a. Chứng minh rằng: A, P, M, H, Q thuộc 1 đường tròn. Xác định tâm O của đường tròn đó.b. Chứng minh rằng: OM vuông góc PQ.c. Chứng minh rằng: MP+MQAHd. Xác định vị trí điểm M sao cho độ dài PQ nhỏ nhất.Giúp mình với....
Đọc tiếp
1. Cho tam giác ABC nội tiếp đương tròn O. Đường cao AD cắt đường tròn tại E, vẽ đường kính AM.
a. Chứng minh rằng: BEMC là hình thang cân
b. Chứng minh rằng: DA2 + DB2 + DE2 + DC2 = 4.R2
2. Cho tam giác ABC đều, đường cao AH, điểm M thuộc BC. Gọi P và Q là hình chiếu của M trên AB, AC.
a. Chứng minh rằng: A, P, M, H, Q thuộc 1 đường tròn. Xác định tâm O của đường tròn đó.
b. Chứng minh rằng: OM vuông góc PQ.
c. Chứng minh rằng: MP+MQ=AH
d. Xác định vị trí điểm M sao cho độ dài PQ nhỏ nhất.
Giúp mình với. Cảm ơn ạ!