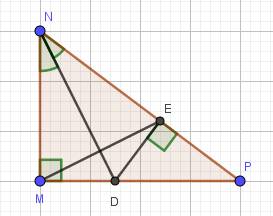
a) Xét hai tam giác vuông: \(\Delta MND\) và \(\Delta END\) có:
ND chung
\(\widehat{MND}=\widehat{END}\) (ND là phân giác của \(\widehat{MNP}\))
\(\Rightarrow\Delta MND=\Delta END\) (cạnh huyền-góc nhọn)
b) Do \(\Delta MND=\Delta END\left(cmt\right)\)
\(\Rightarrow MD=ED\) (hai cạnh tương ứng)
\(\Delta MED\) có MD = ED (cmt)
\(\Rightarrow\Delta MED\) cân tại D
c) Ta có:
\(\widehat{NDP}\) là góc ngoài của \(\Delta MND\)
\(\Rightarrow\widehat{NDP}=\widehat{NMD}+\widehat{MND}\)
\(=90^0+\widehat{MND}\)
\(\Rightarrow\widehat{NDP}\) là góc tù
\(\Delta NDP\) có \(\widehat{NDP}\) là góc tù
Mà góc tù là góc lớn nhất trong tam giác
\(\Rightarrow NP\) là cạnh lớn nhất (quan hệ giữa góc và cạnh đối diện trong \(\Delta NDP\))
\(\Rightarrow ND< NP\)












