ta có: MN2 = NQ x NP = 3 x 9 = 27
=> MN = \(\sqrt{27}=5,196\)
\(sin\widehat{P}=\dfrac{MN}{NP}=\dfrac{5,196}{9}=\approx0,577\)
Đúng 0
Bình luận (0)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
cho tam giac ABC nhon co AB<AC noi tiep duong tron (O),lay M tuy y tren cung BC ke MP vuong voi ACva PR vuong voi BC tai Q,
a)chung minh MQ vuong voi PQ va PM*CM=BM*MR
c)ke duong cao AD va CE cua tam giac ABCcat nhau tai Hduong kinh BK cat DE tai I.cm tu giac DCKI noi tiep duong tron
d)ke SC vuong voi AM tai S.chung minh PQ vuong ES
cho tam giac MNP vuong tai M
MN=6a,MP=8a
khi do tan P bang
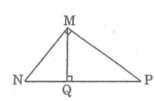
Đường cao MQcuar tam giác vuông MNP chia cạnh huyền NP thành hai đoạn NQ = 3, PQ = 6. Hãy so sánh cotgN và CotgP. Tỉ số nào lớn hơn và lớn hơn bao nhiêu lần?
Đường cao MQ của tam giác vuông MNP chia cạnh huyề NP thành hai đoạn NQ=3,PQ=6.Hãy so sánh cotgN và cotgP . Tỉ số nào lớn hơn và lớn hơn bao nhiêu lần
Đường cao MQ của tam giác vuông MNP chia cạnh huyển NP thành hai đoạn NQ 3, PQ 6. Hãy so sánh cotg
∠
N
và cotg
∠
P
. Tỉ số nào lớn hơn và lớn hơn bao nhiêu lần?
Đọc tiếp
Đường cao MQ của tam giác vuông MNP chia cạnh huyển NP thành hai đoạn NQ = 3, PQ = 6. Hãy so sánh cotg ∠ N và cotg ∠ P . Tỉ số nào lớn hơn và lớn hơn bao nhiêu lần?
Cho tam giác MNP vuông tại M. Từ N dựng đường thẳng NQ về phía ngoài tam giác MNP sao cho NQ=NP và MNP=PNQ và gọi I là trung điểm của PQ , MI cắt NP tại E
1, Chứng minh PMI=QNI
2 Chứng minh tam giác MNE cân
3, Chứng minh MN.PQ=NP.ME
cho tam giac abc vuong tai a,biết ab/ac=5/7,đường cao ah=15cm tính hb,hc
cho tam giac abc vuong tai a duong cao ah. Biết AB:AC=3:4, BC=15cm. Tính BH, HC
Đường cao MQ của tam giác MNP chia cạnh huyền NP thành 2 đoạn NQ = 3 ,PQ = .Hãy so sánh cot N và P