Question

cho tam giác MNP có 2 đường trung tuyến NA;PB và cắt nhau tại G.Chứng minh rằng tam giác MNP cân

Answer 1

`\color{blue}\text {#DuyNam}`

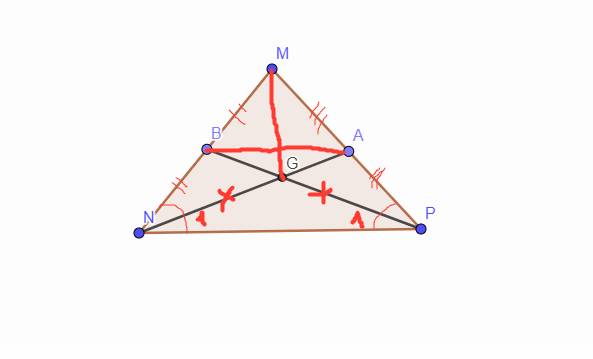
`NA, PB` là đường trung tuyến, cắt nhau tại `G`

`-> G` là trọng tâm của Tam giác `MNP`

`-> GN= 2/3 NA`

`-> GP=2/3 PB`

`NA=PB -> GN = GP`

Xét Tam giác `GNP: GN = GP`

`->` Tam giác `GNP` cân tại `G`.

`->` \(\widehat{N_1}=\widehat{P_1}\) 

Xét Tam giác `NBP` và Tam giác `PAN:`

`NA = PB`

\(\widehat{N_1}=\widehat{P_1}\)

`NP` chung

`=>` Tam giác `NBP =` Tam giác `PAN (c-g-c)`

`=> BN = AP (2` cạnh tương ứng `)`

`-> 1/2 MN = 1/2 MP`

`-> MN = MP`

`->` Tam giác `MNP` cân tại `M`.