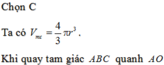Các câu hỏi tương tự
Cho tam giác ABC nội tiếp trong đường tròn tâm O, bán kính R có
B
A
C
^
75
0
,
A
C
B
^
60
0
. Kẻ
B
H
⊥
A
C
. Quay tam giác ABC quanh AC thì tma giác BHC tạo thành hình nón tròn xoa...
Đọc tiếp
Cho tam giác ABC nội tiếp trong đường tròn tâm O, bán kính R có B A C ^ = 75 0 , A C B ^ = 60 0 . Kẻ B H ⊥ A C . Quay tam giác ABC quanh AC thì tma giác BHC tạo thành hình nón tròn xoay (N). Tính diện tích xung quanh của hình nón xoay (N) theo R
A. 3 + 2 2 2 π R 2
B. 3 + 2 3 2 π R 2
C. 3 2 + 1 4 π R 2
D. 3 3 + 1 4 π R 2
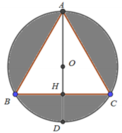
Cho tam giác ABC đều cạnh a và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh khi cho phần tô đậm (hình vẽ) quay quanh đường thẳng AD bằng
Đọc tiếp
Cho tam giác ABC đều cạnh a và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh khi cho phần tô đậm (hình vẽ) quay quanh đường thẳng AD bằng
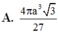
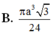
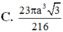
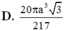
Gọi (H) là hình tròn xoay thu được khi cho tam giác đều ABC có cạnh a quay quanh AB, tính thể tích khối tròn xoay giới hạn bởi (H)
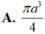

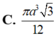
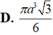
Cho tam giác ABC đều cạnh a và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh ra khi cho phần màu vàng nhạt (hình vẽ bên dưới) quay quanh đường thẳng AD bằng
Đọc tiếp
Cho tam giác ABC đều cạnh a và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh ra khi cho phần màu vàng nhạt (hình vẽ bên dưới) quay quanh đường thẳng AD bằng
![]()
![]()
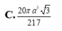
![]()
Tam giác vuông cân ABC ngoại tiếp đường tròn tâm I (như hình vẽ). Cho nửa đường tròn (phần gạch sọc) và tam giác AHC quay quanh AH tạo thành các khối tròn xoay quanh có thể tích là
V
1
,
V
2
. Tính
k
V
1
V
2
.
Đọc tiếp
Tam giác vuông cân ABC ngoại tiếp đường tròn tâm I (như hình vẽ). Cho nửa đường tròn (phần gạch sọc) và tam giác AHC quay quanh AH tạo thành các khối tròn xoay quanh có thể tích là V 1 , V 2 . Tính k = V 1 V 2 .

![]()
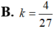
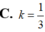
![]()
Cho các đường tròn nội tiếp và ngoại tiếp tam giác đều ABC quay quanh đường cao AH của tam giác tạo nên các khối tròn xoay có thể tích lần lượt là V1, V2. Tính tỉ số
V
1
V
2
Đọc tiếp
Cho các đường tròn nội tiếp và ngoại tiếp tam giác đều ABC quay quanh đường cao AH của tam giác tạo nên các khối tròn xoay có thể tích lần lượt là V1, V2. Tính tỉ số V 1 V 2
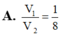
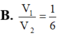
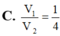
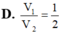
Cho hình trụ có hai đáy là hai hình tròn (O;R) và (O’;R). AB là một dây cung của đường tròn (O;R) sao cho tam giác O’AB là tam giác đều và mặt phẳng (O’AB) tạo với mặt phẳng chứa đường tròn (O;R) một góc
60
°
. Tính theo R thể tích V của khối trụ đã cho
Đọc tiếp
Cho hình trụ có hai đáy là hai hình tròn (O;R) và (O’;R). AB là một dây cung của đường tròn (O;R) sao cho tam giác O’AB là tam giác đều và mặt phẳng (O’AB) tạo với mặt phẳng chứa đường tròn (O;R) một góc 60 ° . Tính theo R thể tích V của khối trụ đã cho
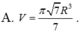
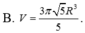
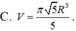
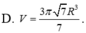
Cho
△
ABC nội tiếp trong đường tròn tâm O, bán kính R có
B
A
C
^
75
∘
,
A
C
B
^
60
∘
. Kẻ BH vuông...
Đọc tiếp
Cho △ ABC nội tiếp trong đường tròn tâm O, bán kính R có B A C ^ = 75 ∘ , A C B ^ = 60 ∘ . Kẻ BH vuông góc với AC. Quay △ ABC quanh AC thì △ BHC tạo thành hình nón tròn xoay. Tính diện tích xung quanh của hình nón tròn xoay này.
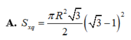
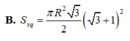
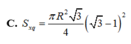
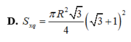
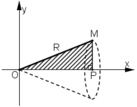
Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Đặt
P
O
M
^
;
O
M
R
0
≤
α
≤
π
3
;
R
0
Gọi V là khối tròn xoay thu được khi quay tam giác đó quanh trụ...
Đọc tiếp
Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Đặt P O M ^ ; O M = R 0 ≤ α ≤ π 3 ; R > 0 Gọi V là khối tròn xoay thu được khi quay tam giác đó quanh trục Ox (H.63).
Tính thể tích của V theo α và R