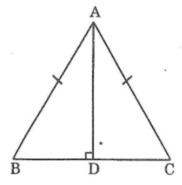
Xét hai tam giác vuông ADB và ADC, ta có:
∠(ADB) =∠(ADC) = 90o
AB = AC (giả thiết)
AD cạnh chung
Suy ra: ΔADB= ΔADC(cạnh huyền, cạnh góc vuông)
⇒ ∠(BAD) =∠(CAD) (hai góc tương ứng)
Vậy AD là tia phân giác ∠(BAC)
Cho tam giác ABC vuông tại A. Từ A kẻ AH vuông góc với BC tại H, tia phân giác của góc CAH cắt BC. Chứng minh rằng:
a) Tam giác ABD cân
b) Các tia phân giác của góc BAH và BHA cắt nhau tại I. Gọi M là trung điểm của AD. Chứng minh B, I, M thẳng hàng
c) Gọi N trung điểm của BC. Chứng minh 2AN = BC
d) A Chứng minh AB + AC = 2AM
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC tại H. Kẻ tia phân giác AD của góc BAH tại D.
a) Chứng minh rằng : Góc BAH = góc C , góc CAH = góc B
b) Chứng minh rằng : Góc DAC = góc ADC
c) Kẻ tia phân giác của góc C cắt AD tại K. Chứng minh rằng CK vuông góc với AD .
Cho tam giác ABC cân tại BC can tai A và AD là phân giác của góc BAC . Từ D kẻ DE vuông góc với AB và DF vuông góc với AC a) Chứng Minh Rằng AD là đường trung trực của BC
Cho tam giác ABC vuông tại A. Tia phân giác của góc B cách AC tại D. Từ D kẻ DH vuông góc với BC (H€BC) và DH cách AB tại K a) Chứng minh AD =DH b) So sánh độ dài cạnh AD và BC c) Chứng minh tam giác KBC là tam giác cân
cho tam giác ABC cân tại A, AD là tia phân giác của góc BAC (D thuộc BC ). a, Chứng minh tam giác ADB = tam giác ADC b, Chứng minh AD vuông góc BC c, Kẻ DM vuông góc AB ,DN vuông góc AC. Chứng minh AM = AN. d, Chứng minh MN // BC.
Cho tam giác ABC cân tại A. Qua B kẻ đường thẳng vuông góc với AB, qua C kẻ đường thẳng vuông góc với AC, chúng cắt nhau tại D. Chứng minh rằng AD là tia phân giác của góc A.
Cho tam giác ABC vuông tại A và AB <AC. Tia phân giác của góc ABC cắt cạnh AC tại D. Kẻ DE vuông góc với BC (điểm E thuộc BC).
a) Chứng minh rằng: Hai tam giác ABD và EBD bằng nhau;
b) Giải thích vì sao tam giác ADE là tam giác cân?
c) Chứng minh: 2.AD>AE;
d) Tia ED cắt tia BA tại F. Chứng minh: BD vuông góc với CF
giúp mình với. Mình cần gấp lắm :
Cho tam giác ABC vuông tại A. Tia phân giác của góc ABC cắt cạnh AC tại D. Qua D kẻ thẳng vuông góc với BC tại E và cắt AB tại F.
a. Chứng mình rằng : AD = ED
b. Chứng minh tam giác FBC là tam giác cân
Cho tam giác ABC vuông tại A, đường phân giác BD. Kẻ AE vuông góc với BD cắt BC tại K.
a. Chứng minh: Tam giác ABK cân tại B
b. Chứng minh rằng: DK vuông góc với BC.
c. Kẻ AH vuông góc với BC. Chứng minh rằng: AK là tia phân giác của góc HAC.
d. Gọi I là giao điểm của AH và BD. Chứng minh rằng: IK // AC.
