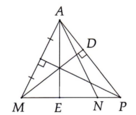
Ta có tam giác AMN cân tại A, do đó A E ⊥ M N . Từ đó d, MD, AE là ba đường cao của AMP, bởi vậy chúng đồng quy. Chú ý: Điểm P ở giữa M và N thì chứng minh không thay đổi.

Ta có tam giác AMN cân tại A, do đó A E ⊥ M N . Từ đó d, MD, AE là ba đường cao của AMP, bởi vậy chúng đồng quy. Chú ý: Điểm P ở giữa M và N thì chứng minh không thay đổi.
Cho tam giác ABC vuông cân tại A. Gọi M là trung điểm của BC.
a) Chứng minh: AM ⊥ BC và MA = MC.
b) Lấy điểm D trên đoạn thẳng AB (D khác A và B), đường thẳng vuông góc với MD tại M cắt AC tại E. Chứng minh: MD = ME.
c) Chứng minh: MD + ME ≥ AD + AE.
Cho tam giác MNP vuông tại M có MN=4cmc ,NP=5cm.Trên tia đối của tia MN lấy điểm A sao cho MN=MA.
a) Chứng minh PN=PA.
b) Gọi B là trung điểm cua AP,đường thẳng NB cắt PM tại G.Tính MP;GP.
c) Đường trung trực của đoạn thẳng MP cắt MP tại I và cắt NP tại C.Chứng minh ba đường thẳng PM,NB và AC đồng quy.
d) Chứng minh IA+IP<NA+NP.
Cho tam giác AMN vuông tại A có AM<AN
a) Cho biết AM=12cm, MN=37cm. Tính độ dài cạnh AN và so sánh các góc trong tam giác AMN
b) Gọi I là trung điểm của AN. Từ điểm I vẽ đường thẳng vuông góc với AN tại I, đường thẳng này cắt MN tại điểm B. Chứng minh tam giác tam giác ABI= tam giác NBI
c) Trên tia đối của tia BA lấy điểm C sao cho BC= BA, CI cắt MN tại D. CHứng minh MN=3ND
Cho tam giác ABC cân ở A có đường cao AH (H thuộc BC)
a, Chứng minh H là trung điểm của BC
b, Kẻ HM vuông góc với AB tại M, HN vuông góc vs AC tại N. Chứng minh tam giác AMN cân ở A
c, Vẽ điểm P sao cho điểm H là trung điểm của đoạn thẳng NP. Chứng minh Đường thẳng BC là đường trung trực của đoạn thẳng MP
d, MP cắt BC tại điểm K. NK cắt MH tại điểm D. Chứng minh Ba đường thẳng AH,MN,DP cùng đi qua 1 điểm
Cho tam giác ABC có ba góc nhọn, AB < AC. Kẻ đường cao AD. Vẽ điểm M sao cho AB là trung trực của DM, vẽ điểm N sao cho AC là trung trực của DN.
a) Chứng minh tam giác AMN cân tại A
b) Đường thẳng MN cắt AB, AC lần lượt tại F, E. Chứng minh DA là tia phân giác của E D F ^ .
c) Chứng minh EB là tia phân giác của D E F ^ .
d) Chứng minh B E ⊥ A C .
e) Chứng minh AD, BE, CF đồng quy.
Cho tam giác AMN vuông tại A có AM<AN. Cho AM=12cm, MN= 37cm
a. Tính độ dài cạnh AN và so sánh các góc của tam giác AMN
b. Gọi I là trung điểm AN. Từ điểm I vẽ đường thẳng vuông góc với An tại I, đường thẳng này cắt MN tại B. Chứng minh Tam giác ABI= tam giác NBI
c. Trên tia dối tia BA lấy điểm C sao cho BC=BA;CI cắt MN tại D. Chứng minh MN=3ND
Cho tam giác ABC cân ở A. Trên BC lấy D, tia đối của CB lấy E sao cho BD=CE. Từ D kẻ đường thẳng vuông góc với BC cắt AB ở M. Từ E kẻ đường thẳng vuông góc với BC cắt AC tại N
a) chứng minh: MD=NE
b) MN cắt BE tại I. Chứng minh I là trung điểm của DE
c) từ C kẻ đường thẳng vuông góc với AC, từ B kẻ đường thẳng vuông góc với AB, chúng cắt nhau tại O. Chứng minh AO là đường trung trực của BC
Câu 7. Cho tam giác MNP cân tại M. Tia phân giác của góc NMP cắt NP tại A.
a) Chứng minh tam giác AMN = tam giác AMP.
b) Kẻ AB vuông góc với MN, AC vuông góc với MP. Chứng minh tam giác ABC
cân.
c) Chứng minh AM vuông góc với BC
d) Kẻ BD vuông góc với NA tại D. Gọi E là giao điểm của đường thẳng BD và MP.
Chứng minh M là trung điểm của CE.