Các câu hỏi tương tự
Cho tam giác ABC vuông tại A và góc ABC = 60o
a) So sánh AB và AC
b) Trên cạnh BC lấy điể D sao cho BD = AB . Qua D kẻ đường thẳng vuông góc với BC cắt tia đối AB tại E . CM : tam giác ABC = tam giác DBE
c) Gọi H là giao điểm của ED và AC . CM : tia BH là tia phân giác góc ABC ?
Bài 1: Cho tam giác ABC, D là trung điểm của AB. Đường thẳng qua D và // với BC cắt AC ở E. Đường thẳng qua E và // với AB cắt BC ở F. CMR:a) AD EFb) Tam giác ADE tam giác EFCBài 2: Cho tam giác ABC, tia phân giác của góc C cắt AB ở D. Trên tia đối của tia CA lấy điểm E sao cho CE CB.a) CM CD//EBb) Tia phân giác của góc E cắt đường thẳng CD tại F. Vẽ CK vuông góc với EF tại K. CM CK là tia phân giác của góc ECFBài 3: Cho tam giác ABC cân tại A, trên tia AB lấy điểm D, trên tia đối của tia CA...
Đọc tiếp
Bài 1: Cho tam giác ABC, D là trung điểm của AB. Đường thẳng qua D và // với BC cắt AC ở E. Đường thẳng qua E và // với AB cắt BC ở F. CMR:
a) AD = EF
b) Tam giác ADE = tam giác EFC
Bài 2: Cho tam giác ABC, tia phân giác của góc C cắt AB ở D. Trên tia đối của tia CA lấy điểm E sao cho CE = CB.
a) CM CD//EB
b) Tia phân giác của góc E cắt đường thẳng CD tại F. Vẽ CK vuông góc với EF tại K. CM CK là tia phân giác của góc ECF
Bài 3: Cho tam giác ABC cân tại A, trên tia AB lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho CE=BD, DE cắt BC tại I. Trên tia đối của tia BC lấy điểm F sao cho BF=CI. CMR:
a) Tam giác BFD = tam giác CIE
b) Tam giác DFI cân
c) I là trung điểm của DE
giúp mình với nhé!
Bài 1: Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H.a, c/m: tam giác AHB tam giác AHCb, Gọi I là trung điểm của cạnh AH. Trên tia đối của tia IB, lấy điểm D sao cho IBID. c/m IBIC, từ đó suy ra AH+BD AB+ACc, Trên cạnh CI lấy điểm E sao cho CEfrac{2}{3}CI. c/m D,E,H thẳng hàngBài 2: Cho tam giác ABC có góc A 60 độ. Tia phân gicas của góc b cái AC tại D, ia phân giác của góc C cắt AB tại e. Các tai phân giác đó cắt nhau tại I. c/m: IDIE
Đọc tiếp
Bài 1: Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H.
a, c/m: tam giác AHB = tam giác AHC
b, Gọi I là trung điểm của cạnh AH. Trên tia đối của tia IB, lấy điểm D sao cho IB=ID. c/m IB=IC, từ đó suy ra AH+BD > AB+AC
c, Trên cạnh CI lấy điểm E sao cho CE=\(\frac{2}{3}\)CI. c/m D,E,H thẳng hàng
Bài 2: Cho tam giác ABC có góc A= 60 độ. Tia phân gicas của góc b cái AC tại D, ia phân giác của góc C cắt AB tại e. Các tai phân giác đó cắt nhau tại I. c/m: ID=IE
1) Cho tam giác ABC vuông tại A ( AB AC ) . Trên tia đối của tia AC lấy điểm D sao cho AD AB. Trên cạnh AB lấy điểm E sao cho AC AEa) Chứng minh rằng : tam giác ABC tam giác ADEb) Gọi M , N lần lượt là trung điểm của DE và BC. Chứng minh tam giác ADM tam giác ABN và tam giác AMN vuông cânc) Qua E kẻ EH vuông góc với BC tại H. Chứng minh rằng 3 điểm D ; E ; H thẳng hàng và CE vuông góc với BD
Đọc tiếp
1) Cho tam giác ABC vuông tại A ( AB > AC ) . Trên tia đối của tia AC lấy điểm D sao cho AD = AB. Trên cạnh AB lấy điểm E sao cho AC = AE
a) Chứng minh rằng : tam giác ABC = tam giác ADE
b) Gọi M , N lần lượt là trung điểm của DE và BC. Chứng minh tam giác ADM = tam giác ABN và tam giác AMN vuông cân
c) Qua E kẻ EH vuông góc với BC tại H. Chứng minh rằng 3 điểm D ; E ; H thẳng hàng và CE vuông góc với BD
Bài 1: Cho tam giac ABC, M là trung điểm cua AB. Đường thẳng qua M và song song với BC cắt AC ở I và song song với AB cắt BC ở k. Chứng minh rằng: a) AMIK b) Tam giác AMI bằng tam giác IKC c) AIIC Bài 2: Cho tam giác ABC vuông tại A. Gọi I là trung điểm BC. Trên tia đối của tia IA lấy điểm D sao cho IDIA a) CMR tam giác BID bằng tam giác CIA b) CMR : BD vuông góc với AB c) Qua A kẻ đường thẳng song song với BC cắt đường thẳng BD tại M. C/M tam giác BAM bằng tam giác ABC d) CMR: AB là tia phân gi...
Đọc tiếp
Bài 1: Cho tam giac ABC, M là trung điểm cua AB. Đường thẳng qua M và song song với BC cắt AC ở I và song song với AB cắt BC ở k. Chứng minh rằng: a) AM=IK b) Tam giác AMI bằng tam giác IKC c) AI=IC Bài 2: Cho tam giác ABC vuông tại A. Gọi I là trung điểm BC. Trên tia đối của tia IA lấy điểm D sao cho ID=IA a) CMR tam giác BID bằng tam giác CIA b) CMR : BD vuông góc với AB c) Qua A kẻ đường thẳng song song với BC cắt đường thẳng BD tại M. C/M tam giác BAM bằng tam giác ABC d) CMR: AB là tia phân giác cuả góc DAM Bài 3: Cho tam giác ABC vuông ở A và AB=AC.Gọi K là trung điểm của BC a) C/M: tam giác AKB bằng tam giác AKC b) C/M: AK vuông góc với BC c) từ C vẽ đường vuông góc với BC cắt đường thẳng AB tại E.C/M EK song song với AK Bài 4: Cho tam giác ABC có AB=AC, kẻ BD vuông góc với AC, CE vuông góc với AB(D thuộc AC, E thuộc AB). Gọi O là giao điểm của BD và CE. CMR a) BD= CE b) tam giác OEB bằng tam giác ODC c) AO là tia phân giác cua góc BAC
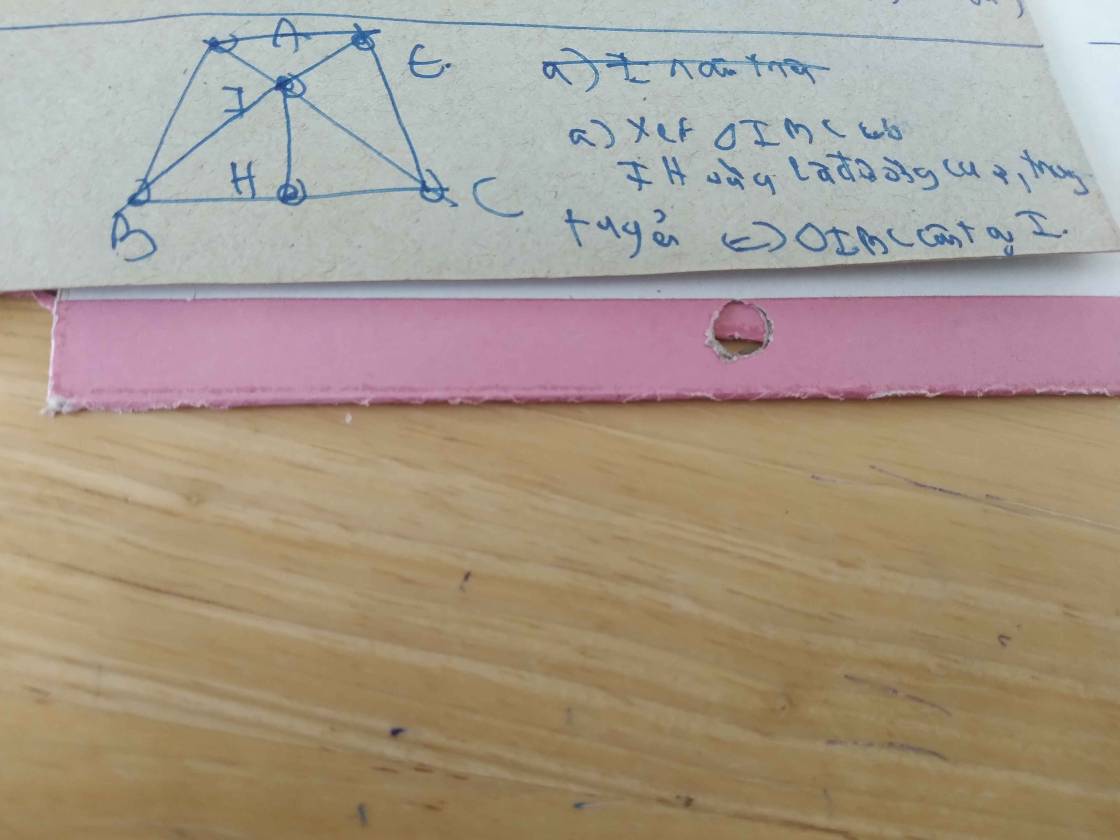
Cho tam giác ABC cân tại A, qua B kẻ đường thẳng vuông góc với AC tại D. tia phân giác của góc BAC cắt BD tại I. Trên AB lấy Điểm E sao cho AE=AD. CM a) IE vuông góc với AB, b) CM ba điểm C,I,E thẳng hàng, c) H là trung điểm của BC, Cm ba điểm A,I,H thẳng hàng
1) Cho tam giác cân ABC (ABAC). Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BDCE. Các đường thẳng vuông góc với BC kẻ từ D và E cắt AB, AC lần lượt ở M,N. DMEN, đường thẳng BC cắt MN tại trung điểm I của MN. Chứng minh rằng: đường thẳng vuông góc vs MN tại I luôn đi qua một điểm cố định khi D thay đổi trên cạnh BC.2)Cho tam giác ABC vuông tại A, K là trung điểm của cạnh BC. Qua K kẻ đường thẳng vuông góc vs AK, đường này cắt các đường thẳng AB và AC lần lượt ở D và E. Gọi...
Đọc tiếp
1) Cho tam giác cân ABC (AB=AC). Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE. Các đường thẳng vuông góc với BC kẻ từ D và E cắt AB, AC lần lượt ở M,N. DM=EN, đường thẳng BC cắt MN tại trung điểm I của MN. Chứng minh rằng: đường thẳng vuông góc vs MN tại I luôn đi qua một điểm cố định khi D thay đổi trên cạnh BC.
2)Cho tam giác ABC vuông tại A, K là trung điểm của cạnh BC. Qua K kẻ đường thẳng vuông góc vs AK, đường này cắt các đường thẳng AB và AC lần lượt ở D và E. Gọi I là trung điểm của DE.
a)Chứng minh rằng: AI vuông góc vs BC
b) Có thể nói DE nhỏ hơn BC được không? Vì sao?
3) Cho tam giác ABC (AB>AC), M là trung điểm của BC. Đường thẳng đi qua M và vuông góc vs tia phân giác của góc A tại H cắt hai tia AB, AC lần lượt tại E và F. CMR:
a) EF^2/4 +AH^2=AE^2
b) 2BME=ACB-B
c) BE=CF
4)Cho tam giác ABC có góc B và C là 2 góc nhọn. Trên tia đối của tia AB lấy điểm D sao cho AD=AB, trên tia đối của tia AC lấy điểm E sao cho AE=AC. M là trung điểm của BE, N là trung điểm CB. Ax là tia bất kỳ nằm gưac 2 tia AB và AC. Gọi H, K lần lượt là hình chiếu của B và C trên tia Ax. Xác định vị trí của tia Ax để tổng BH+CK có giá trị lớn nhất.
5)Cho tam giác ABC có 3 góc nhọn, đường cao AH, ở miền ngoài của tam giác ABC ta vẽ các tam giác vuông cân ABE và ACF đều nhận A làm đỉnh góc vuông. Kẻ EM, FN cùng vuông
góc vs AH (M,N thuộc AH)
a) CM: EM+HC=NH
b) CM: EN // FM
1/ Cho tam giác ABC vuông tại A và góc C bằng 30 độ . Vẽ trung trực của AC , cắt AC tại H và BC tại D , nối ADa)Chứng minh tam giác ABD đều(sẵn vẽ hình giúp mình nhé)b)Kẻ phân giác của góc B cắt AD tại K và cắt DH kéo dài I. CM: I là tâm đường tròn đi qua ba đỉnh của tam giác ADC c)Vẽ IE vuông góc với DC; IF vuông góc với AB kéo dài. CM:IFIEIK2/ Cho tam giác ABC vẽ AH vuông góc với BC. Gọi I và K lần lượt là hình chiếu của H lên AB và AC. Kéo dài HI một đoạn IDHI và kéo dài HK một đoạn KEHK. CM:...
Đọc tiếp
1/ Cho tam giác ABC vuông tại A và góc C bằng 30 độ . Vẽ trung trực của AC , cắt AC tại H và BC tại D , nối AD
a)Chứng minh tam giác ABD đều(sẵn vẽ hình giúp mình nhé)
b)Kẻ phân giác của góc B cắt AD tại K và cắt DH kéo dài I. CM: I là tâm đường tròn đi qua ba đỉnh của tam giác ADC
c)Vẽ IE vuông góc với DC; IF vuông góc với AB kéo dài. CM:IF=IE=IK
2/ Cho tam giác ABC vẽ AH vuông góc với BC. Gọi I và K lần lượt là hình chiếu của H lên AB và AC. Kéo dài HI một đoạn ID=HI và kéo dài HK một đoạn KE=HK. CM:A nằm trên trung trực của DE( vẽ hình giúp mình nhé các bạn )
3/Cho tam giác ABC cân tại A,M và N là hai điểm tương ứng thuộc hai cạnh AB và AC sao cho BM=AN. Gọi O là điểm cách đều ba đỉnh A,B,C .CM: Ocách đều 2 điểm M và N
4/Trên cạnh AB,BC,AC của tam giác đều ABC . Lấy các điểm theo thứ tự M,N,P sao cho AM=BN=CP.Gọi O là giao điểm của 3 đường trung trực của tam giác ABC . CM: O cũng là giao điểm của ba đường trung trực của tam giác MNP
5/Cho tam giác đều ABC . Trên các cạnh BC,CA,AB lần lượt lất các điểm D,E,F sao cho BD=CE=AF.CM:
a)Tam giác AEF đều
b)Các trung trực của ABC và DEF cùng đi qua một điểm
6/Cho tam giác ABC vuông tại A. Tia phân giác BD và CE cắt nhai tại O
a)Chứng tỏ O cách đều ba cạnh của tam giác
b)Từ D và E hạ d8oừng vuông góc xuống BC và cắt CB tại H và K . Tính số đo góc HAk
Mong mọi người vẽ hình và giúp mình giải các bài trên nhé nếu có dài quá thì cho mình xin lỗi
cho tam giác abc có ab=ac. gọi h là trung điểm của cạnh bc. a) Cm tam giác ABC=tam giác ACH và Ah là tia phân giác góc BAC. b) Vẽ HD vuông góc AC tại D. Trên cạnh AB lấy E sao cho AE=AD. Tính góc AED. c) GỌi M là giao điểm AB và DH. Đường thẳng qua M và song song với ED cắt tia AC tại N. Cm N,H,E thẳng hàng