Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến ứng với cạnh huyền BC
nên AM=1/2BC
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho tam giác ABC, vuông tại A, AB<AC. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy D sao cho MA=MD. Kẻ BI và CK cùng vuông góc với AM.
1, CM MI=MK và BK // CI
2, CM BC=2AM
3, CM N là trung điểm của AC
4, Tam giác ABC cần thêm điều kiện gì để AI=IM=MK=KD
Xem chi tiết
Cho tam giác ABC gọi M là trung điểm của cạnh BC trên tia đối của tia MA lấy điểm D sao cho MD = MA A CM AB=CD AC VUÔNG GÓC DC B CM MA=MB=MC C KẺ AH VUÔNG GÓC BC TẠI H CM AH<=BC/2
6: Cho tam giác ABC vuông tại A. Lấy M là trung điểm của BC. Trên tia đối của tia MA lấy
điểm D sao cho MD = MA. Chứng minh rằng:
a) ∆ABC = ∆CDA
b) AM= 1 phần 2 BC
1, Cho tam giác ABC vuông tại A (AB < AC). Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Vẽ AH vuông góc với BC tại H, trên tia đối của tia HA lấy điểm E sao cho HE = HA. Chứng minh rằng: AE vuông góc với ED.
2, Cho tam giác ABC. Gọi M là trung điểm của BC. Vẽ BD vuông góc với AM tại D, CE vuông góc với AM tại E. Chứng minh rằng : AB + AC > 2AM.
cho tam giác vuông vuông tại a có góc c = 30 độ . gọi m là trung điểm của bc , trên tia đối của tia MA lấy điểm d sao cho MD = MA .
a ) CM : △AMB = △DMC
b) CM : △ABC = △CDA
c) CM : △AMB là tam giác đều
Cho tam giác ABC, A = 90 độ, trung tuyến AM, Trên tia đối của MA lấy điểm D sao cho MD = MA. Qua D kẻ xy vuông góc với BC, Trên Ox lấy điểm P trên tia Oy lấy điểm Q sao cho DP = DQ = BC. CM AP, AQ là phân giác trong, phân giác ngoài của tam giác A
Cho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA. So sánh độ dài AM và BC.
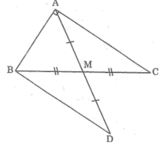
cho tam giác abc vuông tại a.gọi m là trug điểm của bc .trên tia đối của tia ma lấy điểm d sao cho ma=md
a) CMR:tam giác mab=tam giác mdc
b) CMR: ad//cd và tam giác abd=tam giác cda
c) CMR: tam giác abc là tam giác vuông
cho tam giác ABC vuông tại A , M là trung điểm của BC . trên tia đối của MA lấy điểm D sao cho MA = MD
a, chứng minh DC vuông góc với AC
b, chứng minh AM = 1/2 BC