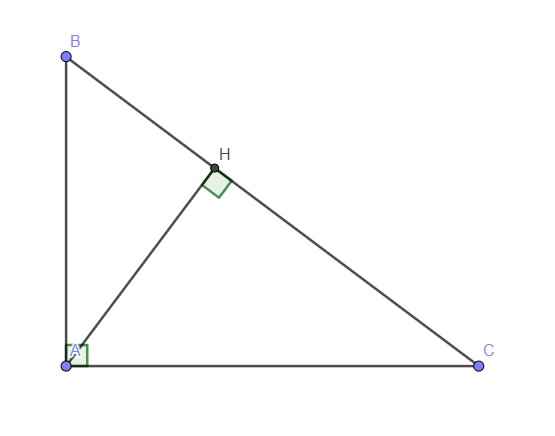
H chắc là chân đường vuông góc hạ từ A xuống BC?
Áp dụng định lý Pitaho cho tam giác vuông ACH:
\(AH=\sqrt{AC^2-CH^2}=6\)
Áp dụng hệ thức lượng cho tam giác vuông ABC:
\(AC^2=CH.BC\Rightarrow BC=\dfrac{AC^2}{CH}=12,5\)
\(\Rightarrow BH=BC-CH=4,5\)
Áp dụng định lý Pitago:
\(AB=\sqrt{BC^2-AC^2}=7,5\)
Xét ΔABC vuông tại A(gt)
=>BC^2=AB^2+AC^2 (theo định lý pytago)
=>BC^2=102+82=164
=>BC≈12,8
Áp dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền ta có:
AB^2=BH⋅BC⇒BH=AB^2/BC=8^2/12,8=5
AC2=HC⋅BC⇒HC=AC^2/BC=10^2/12,8≈7,8
Áp dụng hệ thức liên quan tới đường cao ta có:
AH^2=BH⋅CH=5⋅7,8=39
⇒AH≈6,2
Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:
\(AH^2+HC^2=AC^2\)
\(\Leftrightarrow AH^2=10^2-8^2=36\)
hay AH=6cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow HB=\dfrac{6^2}{8}=4.5\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=BH^2+AH^2\)
\(\Leftrightarrow AB^2=6^2+4.5^2=7.5^2\)
hay AB=7,5cm