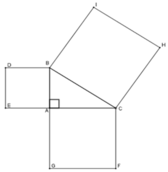
Ta có: SBCHI = BC2; SACFG = AC2; SABDE = AB2
Theo định lý Pytago cho tam giác ABC vuông tại A ta có: BC2 = AB2 + AC2
=> SBCHI = SACFG + SABDE
Đáp án cần chọn là: B

Ta có: SBCHI = BC2; SACFG = AC2; SABDE = AB2
Theo định lý Pytago cho tam giác ABC vuông tại A ta có: BC2 = AB2 + AC2
=> SBCHI = SACFG + SABDE
Đáp án cần chọn là: B
1) Cho tam giác vuông abc tại a . Vẽ phía ngoài tam giác các hình vuông ABDE,ACFG,BCMN.Đường cao AH của tam giác ABC cắt MN ở K. C/m a) S abde=Sbhkn. b) Sacfg=Schkm. 2) cho hbh abcd có m,n,i,k là trung điểm ab,bc,cd,da. ai cắt kb tại e. ai cắt dn tại h. cm cắt kb tại f. cm cắt dn tại g . Cm ae=eh=gc
CHO TAM GIÁC ABC CÓ \(\widehat{A}=90^0\),AM LÀ ĐƯỜNG CAO. VẼ RA BÊN NGOÀI TAM GIÁC CÁC HÌNH VUÔNG ABDE, ACFG, BCHI. A) CM AM*BC=AB*AC VÀ SBCHI=SABDE+SACFG
B) GIẢI CÂU TRÊN, KHÔNG DÙNG ĐỊNH LÍ PYTAGO
Cho tam giác ABC vuông tại A có góc B = 2 lần góc C, đường cao AH ( H thuộc BC )
a) CM tam giác AHB đồng dạng tam giác CAB
b) Tia phân giác của góc ABC cắt AH tại E, cắt AC tại F. CM hệ thức AB^2 = AF.AC
c) CMR HE/EA = AF/FC
d) Biết AB = 2BH. CM S ABC = 3S BEC
S ở câu d là diện tích của tam giác
Các câu a,b,c mình đã giải được nhưng câu d thì chưa, mong các bạn giúp mình
cho hình chữ nhật ABCD,AB=a,BC=b(a>b). Các tia phân giác góc A và B; B và C, C và D,D và A cắt nhau theo thứ tụ E,F,G,H.
a) tính diện tích hình chữ nhật ABCD
b)chứng minh tam giác CDG là tam giác vuông,tính diện tích
p/s Giúp mình nha, mai thi rồi
Mọi người giúp mình với, mình đang cần gấp
1. Cho tam giác ATM vuông tại A (AT<AM), đường cao AB. C thuộc tia BM sao cho BC=BT và CD vuông góc với AM tại D. E là trung điểm của CM. Chứng minh:
a) Tam giác ABD cân
b) BD vuông góc với DE.
2. Cho tam giác ATM nhọn, các đường cao TC và MB cắt nhau tại K. Vẽ TD⊥BC tại D;
ME⊥BC tại E. H là trung điểm của AK, Q là trung điểm của TM.
Chứng minh HC⊥CQ
3. Cho tam giác ABC vuông tại A (AB<AC), trên cạnh BC lấy N sao cho BN=NA, trên cạnh BC lấy M sao cho CM=CA. Tia phân giác góc ABC cắt AM tại E, tia phân giác góc ACB cắt AN tại D. Gọi O là giao của BE và CD, gọi H là giao của MD và NE.
a) Tính góc MAN b) CHứng minh EODH là hình bình hành
c) Gọi K và I lần lượt là trung điểm của AH và MN. Chứng minh IEKD là hình vuông.
4. Cho hình vuông ABCD, E là điểm trên cạnh AB. Trên cùng một đường thẳng bờ là đường thẳng AB có chứa điểm D, dựng các hình vuông AEGH và BEFK. AK cắt BD tại S, AC cắt DE tại T. CHứng minh:
a) AF⊥BG tại M
b) Bốn điểm H, M, K, O thẳng hàng ( O là giao của BD và AC)
c) E, S, C thẳng hàng
d) B, T, H thẳng hàng
5. Cho tam giác ABC nhọn, vẽ ra phía ngoài của tam giác ABC hai hình vuông ABMN và ACEF. Gọi I và K là tâm hình vuông ABMN và ACEF. P,Q là trung điểm của NF và BC. Chứng minh S ABC=S NAF
Cho tam giác ABC vuông tại A( AB<AC), D là trung điểm BC, vẽ DE vuông góc với AB, DF vuong gi s với AC.
a) CM: AFDE là hình chữ nhật
b) Gọi G đối xứng E qua D, H đối xứng F qua D. CM: EFGH là hình thoi
c) CM: HG=1/2 BC
d) BH cắt CG tại I. CM: 3 điểm A, D, I thẳng hàng
Cho tam giác ABC vuông tại A có AB=5cm và AC =12cm. Vẽ đường cao AH và phân giác AD
a)Tính BD và CD
b) Chứng minh tam giác ABH ~tam giác CBA
c)Chứng minh AH2= BH.CH
d)Gọi E,F lần lượt là hình chiếu của H trên AB,AC.Chứng minh rằng nếu SABC=SAEHF thì ABC vuông cân
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E ,F lần lượt là hình chiếu của H trên AB,AC. a) tứ giác AEHF là hình gì.?Vì sao? b) chứng minh tam giác AEF ~tam giác CAB. c) cho AH = 2,4cm, BC=5cm. Tính S tam giác EAF c) lấy I đối xứng với H qua AB. Từ B kẻ đường thẳng vuông góc với AI ở K . Chứng minh KC,AH,EF đồng quy
cho tam giác ABC vuông tại A , D là điểm tùy ý trên cạnh AC . Qua D vẽ đường thẳng vuông góc với BC ở F và cắt đường thẳng AB ở E
a/ Chứng minh tam giác ABC đồng dạng với tam gíc FBE
b/ Chứng minh CD.CA=CF.CB
c/ Gọi G là giao điểm của BD và CE . Chứng minh CD.CA+BD.BG không phụ thuộc vào vị trí điểm D