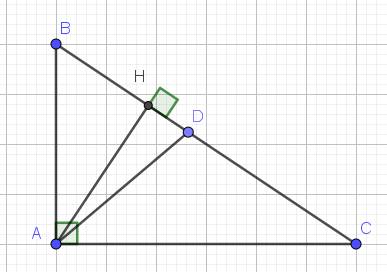
Lời giải:
a. Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{12^2+16^2}=20$ (cm)
Áp dụng tính chất đường phân giác:
$\frac{BD}{DC}=\frac{AB}{AC}=\frac{12}{16}=\frac{3}{4}$
Mà: $BD+DC=BC=20$ nên:
$BD=20:(3+4).3=\frac{60}{7}$ (cm)
$CD= 20:(3+4).4=\frac{80}{7}$ (cm)
b.
$AH=2S_{ABC}:BC=\frac{AB.AC}{BC}=\frac{12.16}{20}=9,6$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{12^2-9,6^2}=7,2$ (cm)
$HD = BD-BH = \frac{60}{7}-7,2=\frac{48}{35}$ (cm)
$AD = \sqrt{AH^2+HD^2}=\sqrt{9,6^2+(\frac{48}{35})^2}=\frac{48\sqrt{2}}{7}$ (cm)
a: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=12^2+16^2=20^2\)
=>\(BC=20\left(cm\right)\)
Xét ΔABC có AD là phân giác
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
=>\(\dfrac{BD}{12}=\dfrac{CD}{16}\)
=>\(\dfrac{BD}{3}=\dfrac{CD}{4}\)
mà BD+CD=BC=20
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{20}{7}\)
=>\(BD=\dfrac{20}{7}\cdot3=\dfrac{60}{7}\left(cm\right);CD=\dfrac{20}{7}\cdot4=\dfrac{80}{7}\left(cm\right)\)
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot20=12\cdot16=192\)
=>\(AH=\dfrac{192}{20}=9,6\left(cm\right)\)
Ta có: ΔAHB vuông tại H
=>\(HB^2+AH^2=AB^2\)
=>\(HB^2=12^2-9,6^2=51,84\)
=>\(HB=\sqrt{51,84}=7,2\left(cm\right)\)
=>HC=BC-HB=12,8(cm)
Vì CD<CH
nên D nằm giữa C và H
=>CD+DH=CH
=>\(DH=12.8-\dfrac{80}{7}=\dfrac{48}{35}\left(cm\right)\)
ΔAHD vuông tại H
=>\(AH^2+HD^2=AD^2\)
=>\(AD^2=\left(\dfrac{48}{35}\right)^2+9,6^2=\dfrac{4608}{49}\)
=>\(AD=\sqrt{\dfrac{4608}{49}}=\dfrac{48\sqrt{2}}{7}\left(cm\right)\)