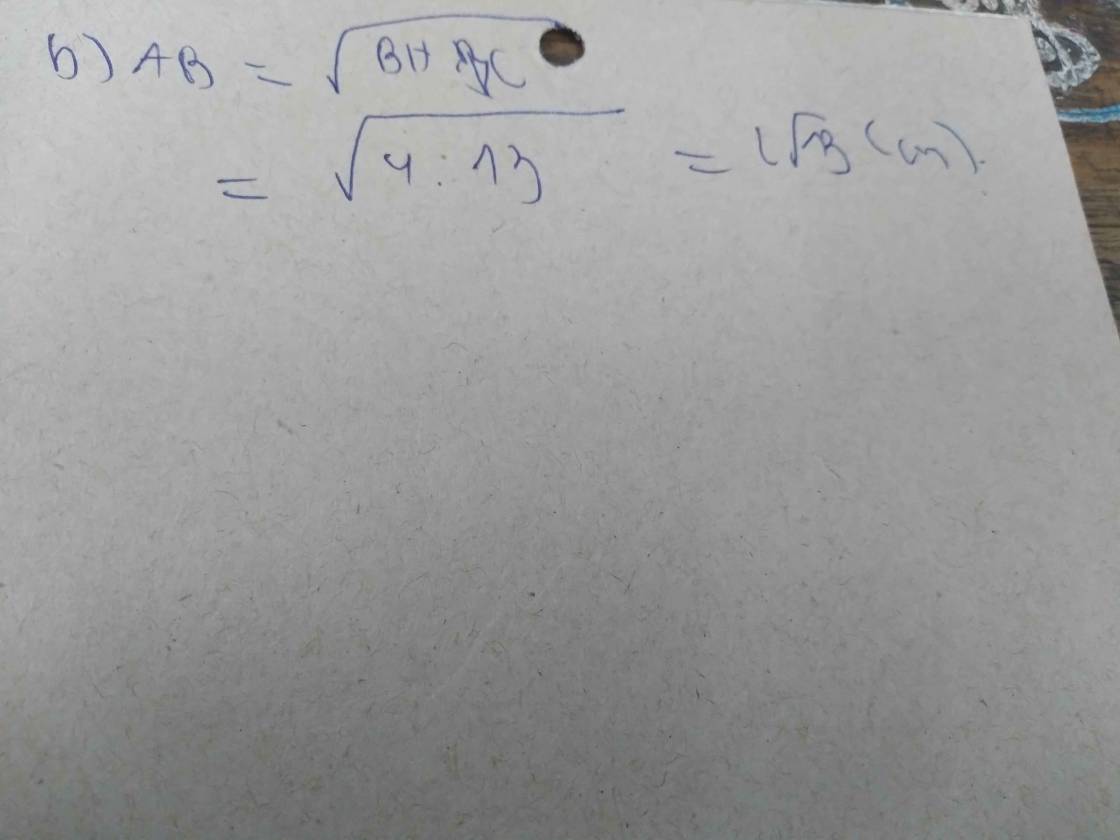Các câu hỏi tương tự
bài 4: Cho tam giác ABC vuông tại A, đường cao AH.
a) CM tam giác ABH đồng dạng với tam giác CBA
b)Cho BH=4cm, BC=9cm. Tính độ dài đoạn AB
c)Gọi E là điểm tùy ý trên cạnh AB, đường thẳng qua H và vuông góc với HE cắt cạnh AC tại F. CM AE.CH=AH.FC
Cho tam giác ABC vuông tại A, đường cao AH.
a) Chứng minh :tam giác ABH đồng dạng với tam giác CBA.
b) Cho BH = 4cm, BC = 13 cm. Tính độ dài đoạn AB.
c) Gọi E là điểm tùy ý trên cạnh AB, đường thẳng qua H và vuông góc với HE cắt cạnh
AC tại F. Chứng minh: AE. CH = AH. FC.
d) Tìm vị trí của điểm E trên cạnh AB để tam giác EHF có diện tích nhỏ nhất.
Cho tam giác ABC vuông tại A, đường cao AH
a) Chứng minh tam giác ABC đồng dạng tam giác HBA
b) Cho BH=4, BC=13. Tính AH, AB
c) Gọi E là 1 điểm tuỳ ý trên AB, đường thẳng qua H và vuông góc với HE cắt cạnh AC tại F. Chứng minh rằng AE.CH=AH.FC
d) Xác định vị trí của E trên AB để đoạn thẳng EF có độ dài ngắn nhất
cho tam giác ABC vuông tại a đường cao AH a) chứng minh tam giác ABC ~ tam giác HBA từ đó suy ra AB^2=BH .BC b) cho BH=4cm CH=9cm tính AH,AB c) gọi F điểm tùy ý trên AC, đường thẳng qua H vuông góc HF cắt cạnh AB tại E chứng minh AE . CH=AH . FC d) xác định vị trí của F trên AC để đoạn FE có độ dài ngắn nhất
Cho tam giác ABC vuông tại A có AB15 cm AC20cm. Vẽ AH vuông góc với BC tại H.1,Chứng minh tam giác HBA và tam giác ABC đồng dạng.2,Tính BC, AH.3,Vẽ tia phân giác của góc BAH cắt BH tại D. Tính BH DH .4, Trên cạnh HC lấy E sao cho HE HA, qua E vẽ đường thẳng vuông góc với cạnh BC cắt AC tại M, qua C vẽ đường thẳng vuông góc với BC cắt tia phân giác của góc MEC tại F. Chứng minh H,M,F thẳng hàng
Đọc tiếp
Cho tam giác ABC vuông tại A có AB=15 cm AC=20cm. Vẽ AH vuông góc với BC tại H.
1,Chứng minh tam giác HBA và tam giác ABC đồng dạng.
2,Tính BC, AH.
3,Vẽ tia phân giác của góc BAH cắt BH tại D. Tính BH DH .
4, Trên cạnh HC lấy E sao cho HE =HA, qua E vẽ đường thẳng vuông góc với cạnh BC cắt AC tại M, qua C vẽ đường thẳng vuông góc với BC cắt tia phân giác của góc MEC tại F. Chứng minh H,M,F thẳng hàng
cho tam giác abc vuông tại A AB=6 cm AC=8 cm Vẽ đường cao AH
a,Chứng minh tam giác AHB đồng dạng với tam giác CAB
b,TÍnh độ dài AH và HB
c,Lấy điểm D bất kì trên cạnh AC Kẻ đường thẳng vuông góc với HD tại H cắt AB tại E Chứng minh tam giác BHE đồng dạng với tam giác AHD,góc BAH=góc EDH
d,Khi D là trung điểm AC tính diện tích tam giác HDE
cho tam giác ABC vuông tại A.Có AB3cm,AC4cm,vẽ đường cao AH.a) Chứng minh rằng tam giác BAC đồng dạng tam giác AHCb)Vẽ đường thẳng vuông góc với AC tại C cắt AH kéo dài tại D. Chứng minh rằng tam giác BAC đồng dạng tam giác ACD và AC^2AB.CDc)chứng minh tứ giác ABCD là hình thang vuông. Tính diện tích ABCDd)Qua H kẻ đường thẳng vuông góc với AC cắt AC tại E và cắt BD tại F .So sánh HE và HF?
Đọc tiếp
cho tam giác ABC vuông tại A.Có AB=3cm,AC=4cm,vẽ đường cao AH.
a) Chứng minh rằng tam giác BAC đồng dạng tam giác AHC
b)Vẽ đường thẳng vuông góc với AC tại C cắt AH kéo dài tại D. Chứng minh rằng tam giác BAC đồng dạng tam giác ACD và AC^2=AB.CD
c)chứng minh tứ giác ABCD là hình thang vuông. Tính diện tích ABCD
d)Qua H kẻ đường thẳng vuông góc với AC cắt AC tại E và cắt BD tại F .So sánh HE và HF?
Cho tam giác ABC vuông tại B có BC >AB, lấy N là một điểm tùy ý trên cạnh AC (N ko trùng với C và A). Qua N kẻ đường thẳng vuông góc với AC và cách đoạn BC tại H , cắt đường thẳng BA tại D
a) chứng minh tam giác ABC đồng dạng tam giác AND
b) chứng minh BC.HC=AC.NC
c. chứng minh rằng góc CBN = góc HAC
d. chứng minh BC là phân giác của góc NBE với E là giao điểm của AH và DC.
cho tam giác ABC vuông tại a,ABlớn hơn AC. M là 1 điểm tùy ý trên cạnh BC.Qua M kẻ đường thẳng vuông góc với BC, đường thẳng này cắt đoạn AB tại E và cắt đường thẳng AC tại F.a, chứng minh tam giác ABC đồng dạng với tam giác MFC.b, chứng minh:BE nhân BA bằng BM nhân BC.c,chứng minh BAM bằng ECB. Gọi K là giao điểm của đường thẳng CE và BF.chứng minh AB là phân giác của góc MAK.giúp e nốt bài này với ạh
Đọc tiếp
cho tam giác ABC vuông tại a,ABlớn hơn AC. M là 1 điểm tùy ý trên cạnh BC.Qua M kẻ đường thẳng vuông góc với BC, đường thẳng này cắt đoạn AB tại E và cắt đường thẳng AC tại F.
a, chứng minh tam giác ABC đồng dạng với tam giác MFC.
b, chứng minh:BE nhân BA bằng BM nhân BC.
c,chứng minh BAM bằng ECB. Gọi K là giao điểm của đường thẳng CE và BF.
chứng minh AB là phân giác của góc MAK.
giúp e nốt bài này với ạh