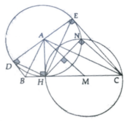
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn (A; AH). Từ B, C kẻ các tiếp tuyến BD, CE với (A) trong đó D, E là các tiếp điểm
a, Chứng minh ba điểm A, D, E thẳng hàng
b, Chứng minh BD.CE = D E 2 4
c, Gọi M là trung điểm CH. Đường tròn tâm M đường kính CH cắt (Ạ) tại N với N khác H. Chứng minh CN và AM song song
a, Chú ý: Ab là phân giác góc D A M ^ ; AC là phân giác góc E A M ^ từ đó D A E ^ = 180 0
b, Sử dụng tính chất hai tiếp tuyến và hệ thức về đường cao và hình chiếu cạnh góc vuông lên cạnh huyền trong tam giác vuông BAC => BD.CE = BH.CH = C H 2 = D E 2 4
c, ∆HNC nội tiếp đường tròn (M) đường kính HC => HN ⊥ NC
Chứng minh AN là tiếp tuyến của (M)
Do đó AM ⊥ HN => AM//NC











