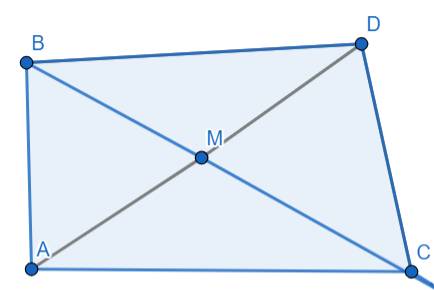
a) \(\Delta ABC\) vuông tại A áp dụng định lý Py-ta-go ta có:
\(BC=\sqrt{AC^2+AB^2}=\sqrt{15^2-8^2}=17\left(cm\right)\)
b) Xét \(\Delta ABM\) và \(\Delta DMC\) ta có:
\(MA=MD\left(gt\right)\)
\(\widehat{BMA}=\widehat{DMC}\) (hai góc đổi đỉnh)
\(BM=MC\) (M là trung điểm của BC)
\(\Rightarrow\Delta ABM=\Delta DMC\left(c-g-c\right)\)