Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=16\)
hay AC=4cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=1.8cm\\CH=3.2cm\\AH=2.4cm\end{matrix}\right.\)
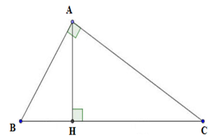
Xét tam giác ABC vuông tại A
+ Theo định lý Pytago ta có:
+ Theo hệ thức lượng trong tam giác vuông ta có:
A B 2 = BH. BC => BH = A B 2 B C = 3 2 5 = 9 5 = 1 , 8 c m
Mà BH + CH = BC => CH = BC – BH = 5 – 1,8 = 3,2 cm
Lại có AH. BC = AB.AC => AH = A B . A C B C = 3.4 5 = 2,4cm
Vậy BH = 1,8cm, CH = 3,2cm, AC = 4cm, AH = 2,4 cm












