Chọn C.
Vì ![]() nên
nên
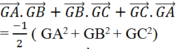
Gọi M, N, P lần lượt là trung điểm của BC, CA, AB
Tam giác ABM đều nên ![]()
Theo định lý Pitago ta có:
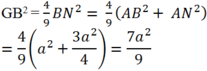
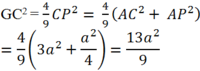
Suy ra
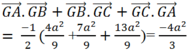
Chọn C.
Vì ![]() nên
nên
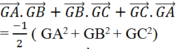
Gọi M, N, P lần lượt là trung điểm của BC, CA, AB
Tam giác ABM đều nên ![]()
Theo định lý Pitago ta có:
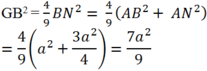
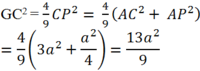
Suy ra
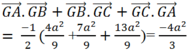
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(2;4), trọng tâm G ( 2 ; 2 3 ) . Biết rằng đỉnh B nằm trên đường thẳng d: x + y + 2 = 0 và đỉnh C có hình chiếu vuông góc trên d là điểm H(2;-4). Giả sử B(a;b). Tính giá trị của biểu thức P = a - 3b.
Câu 4 : Cho tam giác ABC vuông cân tại A và AB =√2 . Tính vectơ CA . vectơ BC . Câu 5 : Cho ABC có trọng tâm G . Biểu diễn vectơ AG theo hai vectơ AB , AC được kết quả là? Câu 6 : Cho các vectơ a,b thỏa mãn|vectơ a | =1 , |vectơ B | =2 , | vectơ a - vectơ b| =3 . Tích vectơ a. vectơ b bằng? Câu 7 : Cho hình vuông ABCD có cạnh bằng a . Tính| vectơ AB - vectơ AD + vectơ CD | .
Cho ba điểm A(4; 3), B(2; 7) và C(-3; -8).
a, Tìm tọa độ trọng tâm G và trực tâm H của tam giác ABC;
b, Gọi T là tâm đường tròn ngoại tiếp tam giác ABC. Chứng minh T, G và H thẳng hàng.
c, Viết phương trình đường tròn ngoại tiếp tam giác ABC.
Cho tam giác ABC có AB=4, AC = 5 , BAC =120°. G là trọng tâm của tam giác ABC, điểm E thỏa mãn vector AE=2/3 vector EC
a) Biểu diễn BE theo AB,AC.
b) Tìm tập hợp điểm I thỏa mãn đẳng thức vec tơ |IA+IG|=|IA–IG|.
c) M là một điểm khác G thỏa(GC-GB)(MA+MB+MC)=0. Chứng minh MG vg BC.
vector het nha
Cho 3 điểm A(-1;2), B(0;4), C(3;2). a) Tính tọa độ AB , AC, BC và diện tích tam giác ABC. b) Tính tọa độ trung điểm I của cạnh AB, trọng tâm G tam giác ABC. c) viết pt tổng quát và tham số của cạnh AB, BC, AC. d) Viết pt tổng quát và tham số của đường thẳng d qua A và song song BC. e) Viết pt đường tròn có tâm B và qua A. f) Viết pt tiếp tuyến của đường tròn (C) vừa tìm được biết tiếp tuyến vuông góc BC.
Cho tam giác ABC có A(1; 2), B(–2; 6), C(9; 8).
a Tính . Cm tam giác ABC vuông tại A.
b Tìm tâm và bán kính đường tròn ngoại tiếp tam giác ABC.
c Tìm toạ độ trực tâm H và trọng tâm G của tam giác ABC.
d Tính chu vi, diện tích tam giác ABC.
e Tìm toạ độ điểm M trên Oy để B, M, A thẳng hàng.
f Tìm toạ độ điểm N trên Ox để tam giác ANC cân tại N.
g Tìm toạ độ điểm D để ABDC là hình chữ nhật.
h Tìm toạ độ điểm K trên Ox để AOKB là hình thang đáy AO.
Cho hai tam giác $A B C$ và $A_{1} B_{1} C_{1}$ có cùng trọng tâm $\mathrm{G}$. Gọi $G_{1}, G_{2}, G_{3}$ lần lượt là trọng tâm tam giác $B C A_{1}, A B C_{1}, A C B_{1}$. Chứng minh rằng $\overrightarrow{G G_{1}}+\overrightarrow{G G_{2}}+\overrightarrow{G G_{3}}=\overrightarrow{0}$
Cho tam giác ABC, A(4;0) B(2;-4) C(0;-2). Gọi G là trọng tâm tam giác ABC. GỌi M, N, P lần lượt là trung điểm các cạnh BC, CA, AB. Chứng minh tam giác ABC, tam giác MNP có cùng trọng tâm
cho 4 điểm a b c d g là trọng tâm của tam giác abc b là trọng tâm của DG chứng minh rằng DA-5DB+DC=0