Question

Cho tam giác ABC vuông tại A có AB = 15cm; AC = 20cm. Gọi D là trung điểm AB và M là trung điểm BC.

Tính BC và DM.

Gọi I là trung điểm MD và E là trung điểm AC. Chứng minh: BDEM là hình bình hành và B, I, E thẳng hàng.

Gọi O là giao điểm của AM và DE, gọi N là trung điểm BD. Chứng minh: Tứ giác AOIN là hình thang cân.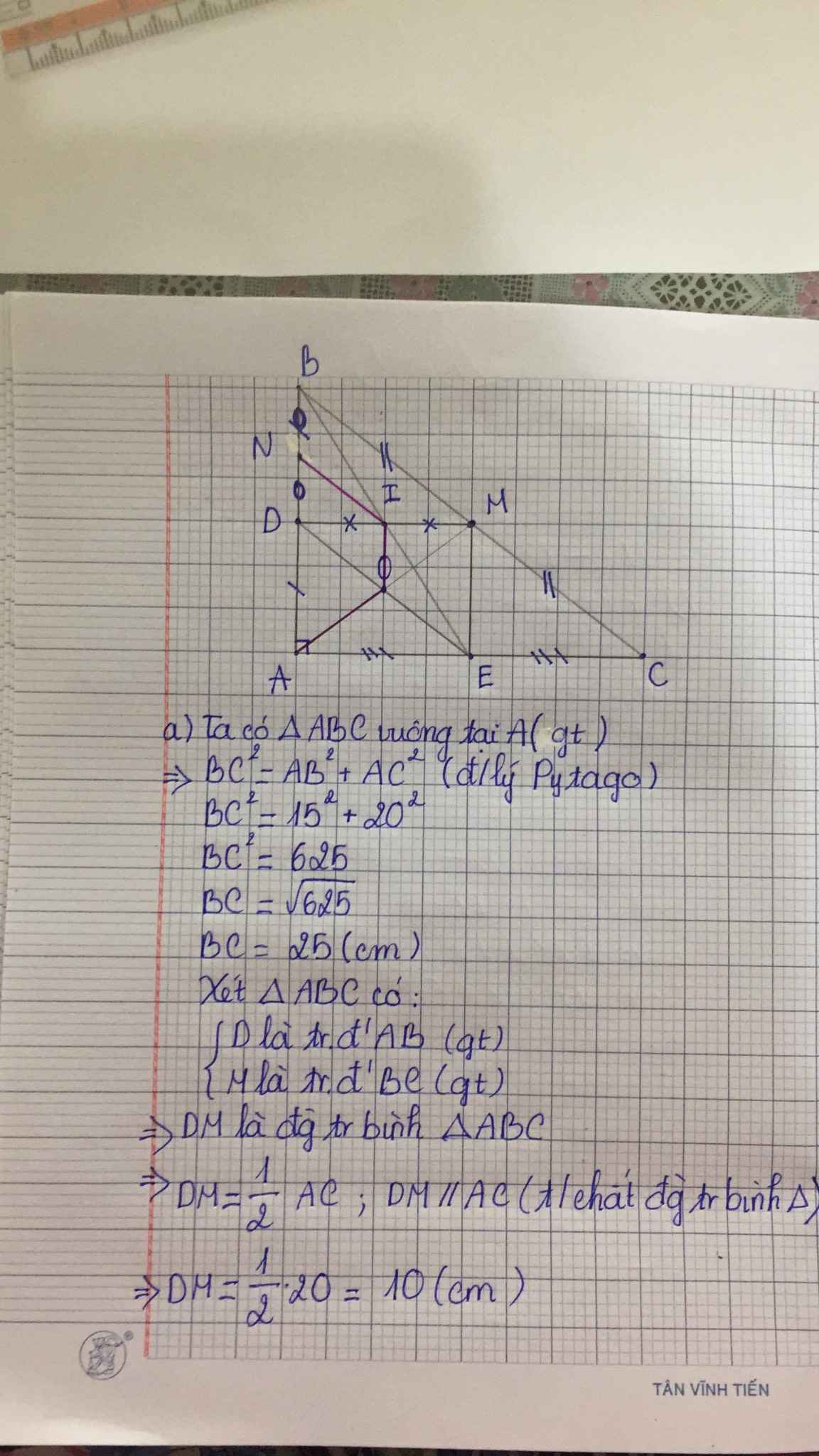

Answer 1

a: Xét ΔABC vuông tại A có \(BC^2=AB^2+AC^2\)

hay BC=25(cm)

Xét ΔABC có 

D là trung điểm của AB

M là trung điểm của BC

Do đó: DM là đường trung bình của ΔABC

Suy ra: \(DM=\dfrac{AC}{2}=10\left(cm\right)\)