Các câu hỏi tương tự
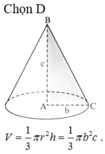
Cho tam giác ABC vuông tại A. ABc, ACb. Quay tam giác ABC xung quanh đường thẳng chứa cạnh AB được một hình nón có thể tích bằng:
Đọc tiếp
Cho tam giác ABC vuông tại A. AB=c, AC=b. Quay tam giác ABC xung quanh đường thẳng chứa cạnh AB được một hình nón có thể tích bằng:
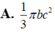
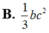
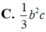
Cho
∆
ABC vuông tại A có AB 3, AC 4. Quay tam giác quanh AB ta được hình nón tròn xoay có diện tích xung quanh
S
1
và quay tam giác quanh AC ta thu được hình nón xoay có diện tích xung quanh
S
2
. Tính tỉ số
S
1
S
2
A.
4
3...
Đọc tiếp
Cho ∆ ABC vuông tại A có AB = 3, AC = 4. Quay tam giác quanh AB ta được hình nón tròn xoay có diện tích xung quanh S 1 và quay tam giác quanh AC ta thu được hình nón xoay có diện tích xung quanh S 2 . Tính tỉ số S 1 S 2
A. 4 3
B. 3 4
C. 4 5
D. 3 5
Trong không gian cho tam giác ABC vuông tại A có ABa và BC2a. Quay tam giác ABC xung quanh cạnh AB ta thu được khối nón có thể tích bằng A.
π
a
3
.
B.
3
π
a
3
.
C.
3
3
π
a
3
.
D.
2
3
π
a...
Đọc tiếp
Trong không gian cho tam giác ABC vuông tại A có AB=a và BC=2a. Quay tam giác ABC xung quanh cạnh AB ta thu được khối nón có thể tích bằng
A. π a 3 .
B. 3 π a 3 .
C. 3 3 π a 3 .
D. 2 3 π a 3 .
Cho tam giác ABC vuông tại A, cạnh AB4, BC5. Quay tam giác ABC quanh AB được khối nón có thể tích
V
1
, quay tam giác ABC quanh AC được khối nón có thể tích
V
2
thì A.
V
1
V
2
12
π
B.
V
1
V
2
C. ...
Đọc tiếp
Cho tam giác ABC vuông tại A, cạnh AB=4, BC=5. Quay tam giác ABC quanh AB được khối nón có thể tích V 1 , quay tam giác ABC quanh AC được khối nón có thể tích V 2 thì
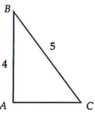
A. V 1 = V 2 = 12 π
B. V 1 > V 2
C. V 1 = V 2 = 16 π
D. V 1 < V 2
Cho tam giác ABC vuông cân tại B, cạnh AB 2. Quay đường gấp khúc ACB quanh cạnh AB ta được hình nón. Tính diện tích xung quang của hình nón đó A.
8
π
2
.
B.
4
π
2
.
C.
4
π
3
.
D.
2
π
2
.
Đọc tiếp
Cho tam giác ABC vuông cân tại B, cạnh AB = 2. Quay đường gấp khúc ACB quanh cạnh AB ta được hình nón. Tính diện tích xung quang của hình nón đó
A. 8 π 2 .
B. 4 π 2 .
C. 4 π 3 .
D. 2 π 2 .
Cho tam giác ABC vuông tại A và có AB4, AC5. Tính thể tích của khối nón sinh ra khi tam giác ABC quay xung quanh cạnh AB
Đọc tiếp
Cho tam giác ABC vuông tại A và có AB=4, AC=5. Tính thể tích của khối nón sinh ra khi tam giác ABC quay xung quanh cạnh AB
![]()
![]()
![]()
![]()
Cho tam giác ABC vuông tại A, AB6cm, AC8cm. Gọi
V
1
là thể tích khối nón tạo thành khi quay tam giác ABC quanh cạnh AB và
V
2
là thể tích khối nón tạo thành khi quay tam giác ABC quanh cạnh AC. Khi đó, tỷ số
V
1
V
2
bằng:
Đọc tiếp
Cho tam giác ABC vuông tại A, AB=6cm, AC=8cm. Gọi V 1 là thể tích khối nón tạo thành khi quay tam giác ABC quanh cạnh AB và V 2 là thể tích khối nón tạo thành khi quay tam giác ABC quanh cạnh AC. Khi đó, tỷ số V 1 V 2 bằng:
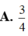
![]()
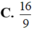
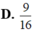
Cho tam giác ABC vuông tại A, AB6cm, AC8cm. Gọi
V
1
là thể tích khối nón tạo thành khi quay tam giác ABC quanh cạnh AB và
V
2
là thể tích khối nón tạo thành khi quay tam giác ABC quanh cạnh AC. Khi đó tỷ số
V
1
V
2
bằng A.
16
9
B. ...
Đọc tiếp
Cho tam giác ABC vuông tại A, AB=6cm, AC=8cm. Gọi V 1 là thể tích khối nón tạo thành khi quay tam giác ABC quanh cạnh AB và V 2 là thể tích khối nón tạo thành khi quay tam giác ABC quanh cạnh AC. Khi đó tỷ số V 1 V 2 bằng
A. 16 9
B. 4 3
C. 3 4
D. 9 16
Cho tam giác ABC cân tại A, góc
B
A
C
^
120
o
và AB 4cm Tính thể tích khối tròn xoay lớn nhất có thể khi ta quay tam giác ABC xung quanh đường thẳng chứa một cạnh của tam giác ABC.
Đọc tiếp
Cho tam giác ABC cân tại A, góc B A C ^ = 120 o và AB = 4cm Tính thể tích khối tròn xoay lớn nhất có thể khi ta quay tam giác ABC xung quanh đường thẳng chứa một cạnh của tam giác ABC.
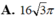
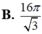
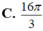
![]()