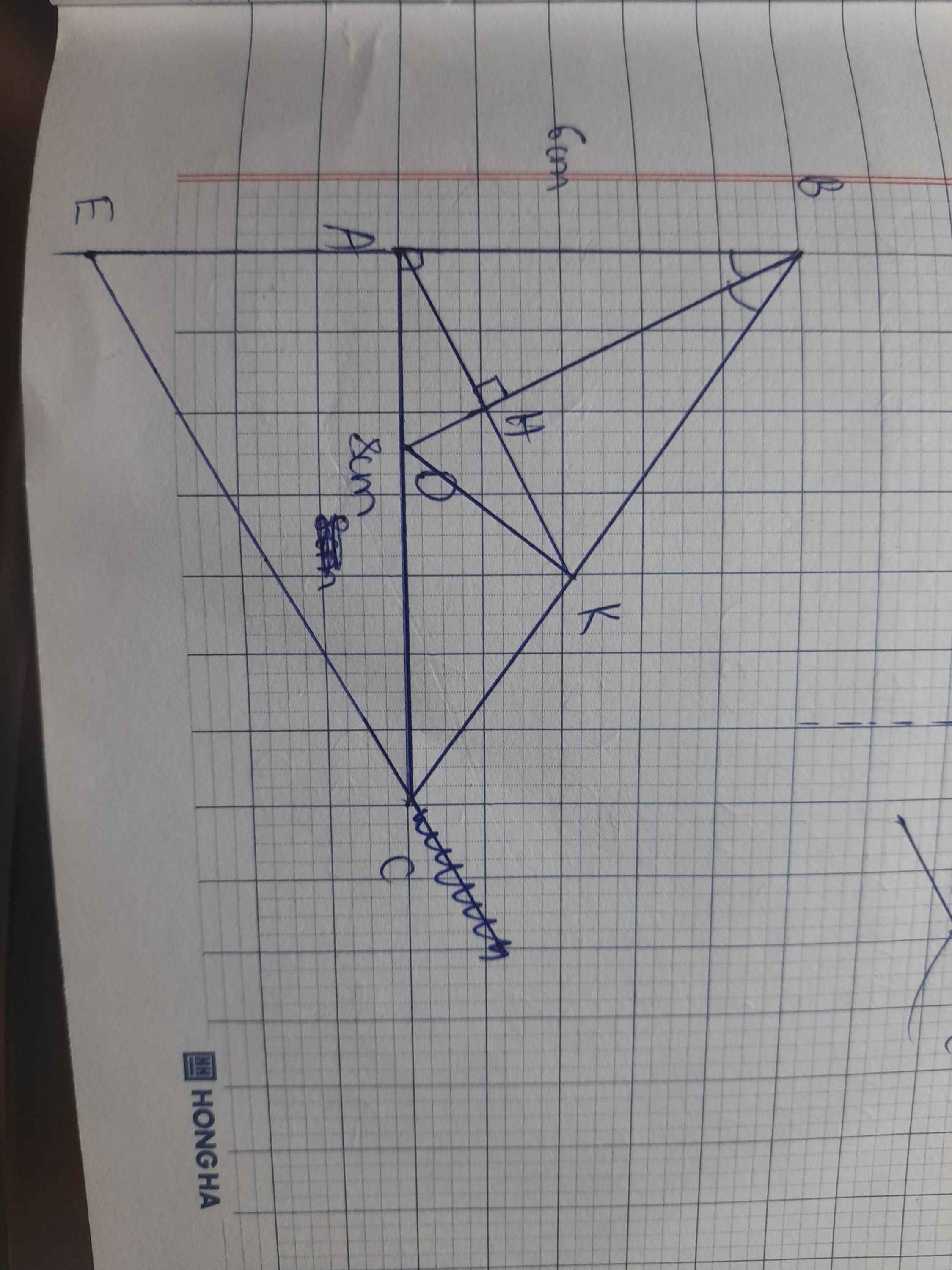
Cho tam giác ABC vuông tại A (AB<AC). Phân giác của góc ABC cắt AC tại D. Trên BC lấy điểm E sao cho BE=BA.
a) Chứng minh rằng: tam giác BDA=tam giác BED.
b) Kẻ AH vuông góc với BC (H thuộc BC), gọi I là giao điểm của AH và BD. Chứng minh I là trực tâm của tam giác ABE.
c) Chứng minh rằng: góc HAE = góc CAE.
#Helpme:>
*Hình
*Bài giải:
Gọi V là giao điểm của BD và AE
a)Xét ▲BDA và ▲BDE có:
AB=BE(GT)
^B1=^B2(BD là tia phân giác của ^B)
BD là cạnh chung
Do đó▲BDA=▲BDE(c-g-c)(ĐPCM)
b)Xét ▲ABV và ▲AEV có:
AB=AE(GT)
^B1=^B2(BD là T.P.G của ^B)
BV là cạnh chung
Do đó▲ABV=▲AEV(c-g-c)
c)Mình không biết làm khó quá chắt cần vẽ thêm đường phụ
=>^BVA=^EVA(2 góc tương ứng)
Mà^BVA+^EVA=180o(kề bù)
=>^BAV=^EVA=180o/2=90o
Ta có:▲BAV có ^V=90o(CMT)
=>BV⊥AE
Trong▲ABE có: AH⊥BC(GT), BV⊥AE(CMT). Mà hai đường thẳng AH và BV cắt nhau tại I. Nên I là trực tâm của ▲ABE(ĐPCM)
Á cái phần c chuyển xuống dưới cùng nha mình nhầm