Các câu hỏi tương tự
cho tam giác nhọn ABC. Đường tròn tâm O đường kính BC cắt các cạnh AB,AC lần lượt tại các điểm M,N . Gọi H là gia điểm BN, CM; P là giao điểm AH và BC1. Chứng minh tứ giác AMHN nội tiếp đường tròn2. Chứng minh BM.BABP.BC3. Trong trường hợp đặc biệt khi tam giác ABC đều cạnh bằng 2a. Tính chu vi đường tròn ngoại tiếp tứ giác AMHN theo a4. Từ A kẻ các tiếp tuyển AE và AF của đường tròn tâm O đường kính BC ( E,F là các tiếp điểm). Chứng minh ba điểm E,H,F thằng hàng Cho tam giác ABC có 3 góc nhọn n...
Đọc tiếp
cho tam giác nhọn ABC. Đường tròn tâm O đường kính BC cắt các cạnh AB,AC lần lượt tại các điểm M,N . Gọi H là gia điểm BN, CM; P là giao điểm AH và BC
1. Chứng minh tứ giác AMHN nội tiếp đường tròn
2. Chứng minh BM.BA=BP.BC
3. Trong trường hợp đặc biệt khi tam giác ABC đều cạnh bằng 2a. Tính chu vi đường tròn ngoại tiếp tứ giác AMHN theo a
4. Từ A kẻ các tiếp tuyển AE và AF của đường tròn tâm O đường kính BC ( E,F là các tiếp điểm). Chứng minh ba điểm E,H,F thằng hàng
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn C tâm O bán kính R. Hai đường cao AE và BK của tam giác ABC cắt nhau tại H ( với E thuộc BC, K thuộc AC)
1. Chứng minh tg AEBK nội tiếp đường tròn
2. Chứng minh CE.CB=CK.CA
3. Chứng minh góc OCA = góc BAE
Cho tam giác ABC cân tại A, D thuộc AB, E thuộc AC, AD = AC, từ E kẻ EK // AB, K thuộc AB, AK giao với DE tài M. Vẽ đường tròn tâm M bán kính MK, đường thẳng này cắt BC tại H ( H khác K )
a) C/m: M là trung điểm của AK và DE
b) C/m: H là trung điểm của BC
Bài 1: Cho tam giác ABC vuông tại A có đường cao AH, trung tuyến BM, phân giác CD đồng quy tại O. Tính tỉ lệ AB/AC.Bài 2: Cho hình vuông ABCD. O là giao của AC và BD. M là điểm bất kì nằm trên tia đối của tia CB. AM cắt CD tại E. OM cắt BE tại I. Chứng minh rằng ∠OIB45 độ.Bài 3: Cho tam giác ABC có trực tâm H, tâm đường tròn ngoại tiếp O. Qua O kẻ đường thẳng song song với BC cắt AC, AB lần lượt tại E, F. Gọi I là trung điểm AH. Chứng minh rằng ∠BIE∠CIF90 độ.
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại A có đường cao AH, trung tuyến BM, phân giác CD đồng quy tại O. Tính tỉ lệ AB/AC.
Bài 2: Cho hình vuông ABCD. O là giao của AC và BD. M là điểm bất kì nằm trên tia đối của tia CB. AM cắt CD tại E. OM cắt BE tại I. Chứng minh rằng ∠OIB=45 độ.
Bài 3: Cho tam giác ABC có trực tâm H, tâm đường tròn ngoại tiếp O. Qua O kẻ đường thẳng song song với BC cắt AC, AB lần lượt tại E, F. Gọi I là trung điểm AH. Chứng minh rằng ∠BIE=∠CIF=90 độ.
Cho tam giác ABC vuông tại A. Đường phân giác góc B cắt AC tại D, cho AB= 6cm, BC= 10cm
a) Tính AC, AD, CD
b) Từ D kẻ đường thẳng vuông góc với AC cắt BC tại K. Qua K kẻ đường thẳng vuông góc với BD tại E và cắt AB, AC lần lượt tại F,H. Chứng minh tam giác ABC đồng dạng tam giác DHK
C) Chứng minh BFDK: hình thoi
Giúp mình 2 bài này với :
1. Cho tam giác ABC (AB<AC). D,E là các điểm lần lượt thuộc AB,AC sao cho BD=CE. DE cắt BC tại K. Chứng minh : AB/AC = KE/KD.
2. Cho tam giác ABC vuông cân tại A, BD là trung tuyến. Qua A kẻ đường thẳng vuông góc với BD cắt BC tại E. Chứng minh EB=2EC
Bài 1: Cho đường tròn tâm O đường kính AB. Lấy C thuộc đường tròn tâm O, C khác A, C khác B. Trên cùng nủa mặt phẳng bờ AB có chứa C kẻ Ax vuông góc với AB. Gọi BC cắt Ax tại D.CMRa) Tam giác ABC vuôngb) BC.BDAB2 không đổi c) Tìm vị trí của điểm C để diện tích tam giác ABC lớn nhấtd) Qua C kẻ đường thẳng vuông góc với OC cắt AD tại E, kẻ CH vuông góc với AB, CH cắt BE tại K. Chứng minh K là trung điểm của CHAi giỏi hình giúp m với, cần trong 2 tiếng nữa ạ :((
Đọc tiếp
Bài 1: Cho đường tròn tâm O đường kính AB. Lấy C thuộc đường tròn tâm O, C khác A, C khác B. Trên cùng nủa mặt phẳng bờ AB có chứa C kẻ Ax vuông góc với AB. Gọi BC cắt Ax tại D.CMR
a) Tam giác ABC vuông
b) BC.BD=AB2 không đổi
c) Tìm vị trí của điểm C để diện tích tam giác ABC lớn nhất
d) Qua C kẻ đường thẳng vuông góc với OC cắt AD tại E, kẻ CH vuông góc với AB, CH cắt BE tại K. Chứng minh K là trung điểm của CH
Ai giỏi hình giúp m với, cần trong 2 tiếng nữa ạ :((
bài hình hay!cho tam giác ABC nhọn có ABAC. đường tròn (O) đường kính BC cắt AB, AC lần lượt tại E,D. BD cắt CE tại H. Các tiếp tuyến tại B, tại D của đường tròn (O) cắt nhau tại K. AK cắt BC tại M. MH cắt BK tại N. Vẽ tiếp tuyến AS đến đường tròn (O) (S thuộc cung nhỏ CD). DB cắt AH tại Ichứng minh rằng a) N,E,I thẳng hàng b) M,E,D thằng hàng c) M,H,S thẳng hàng
Đọc tiếp
bài hình hay!
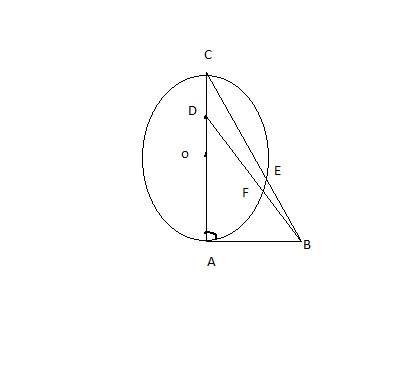
cho tam giác ABC nhọn có AB<AC. đường tròn (O) đường kính BC cắt AB, AC lần lượt tại E,D. BD cắt CE tại H. Các tiếp tuyến tại B, tại D của đường tròn (O) cắt nhau tại K. AK cắt BC tại M. MH cắt BK tại N. Vẽ tiếp tuyến AS đến đường tròn (O) (S thuộc cung nhỏ CD). DB cắt AH tại I
chứng minh rằng a) N,E,I thẳng hàng
b) M,E,D thằng hàng
c) M,H,S thẳng hàng
vẽ hình cm giúp vs !!!
C5: Cho tam giác ABC vuông tại A biết AB = 15cm, AC = 20cm. Kẻ AH vuông góc BC tại D
b) Vẽ tia phân giác của góc BAH cắt BH tại D
c) Trên HC lấy điểm E sao cho HE = HA qua E vẽ đường thẳng vuông góc với BC và cắt AC tại M và qua C vẽ đường thẳng vuông góc với BC cắt theo phân giác của góc MEC tại F. CM: 3 điểm H ,M,F thẳng hàng
Xem chi tiết
1)Cho lục giác đều ABCD. TÌm vị trí của điểm M nằm trong lục giác để: Diện tích tam giác MAC Diện tích tam giác MCD.2)Trên đường tròn tâm O bán kính 15 cm, lấy hai điểm A, B . Đường cao OH của tam giác OAB cắt đường tròn tại C. Tính AC nếu AB16cm.3) Trong tam giác ABC, PQ//BC ( P thuộc AB, Q thuộc AC). Đường thẳng PC và QB cắt nhau tại G. lấy điểm E, F lần lượt nằm trên AB, AC và G thuộc EF sao cho EF//BC với PQa và EFb. Tính BC.
Đọc tiếp
1)Cho lục giác đều ABCD. TÌm vị trí của điểm M nằm trong lục giác để: Diện tích tam giác MAC = Diện tích tam giác MCD.
2)Trên đường tròn tâm O bán kính 15 cm, lấy hai điểm A, B . Đường cao OH của tam giác OAB cắt đường tròn tại C. Tính AC nếu AB=16cm.
3) Trong tam giác ABC, PQ//BC ( P thuộc AB, Q thuộc AC). Đường thẳng PC và QB cắt nhau tại G. lấy điểm E, F lần lượt nằm trên AB, AC và G thuộc EF sao cho EF//BC với PQ=a và EF=b. Tính BC.
Cho tam giác ABC vuông tại A, AB<AC từ điểm D thuộc BC kẻ đường thẳng vuông tại BC cắt AC tại F, AB tại E
a) Chứng minh: tam giác AEF đồng dạng tam giác DCF
b) Chứng minh: AE.BC=EF.AC