Question

Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác của góc ABCcắt ACtạiD.Trên cạnh BC lấy điểm E sao cho BA = BE. a) Chứng minh tam giác BAD = tam giác BED . b) Góc BED là góc gì? Vì sao? c) DE cắt AB tại điểm I. Chứng minh BD vuông góc IC

Nhớ vẽ hình nữa nha.

Ai làm xong nhanh mik sẽ vote 

Answer 1

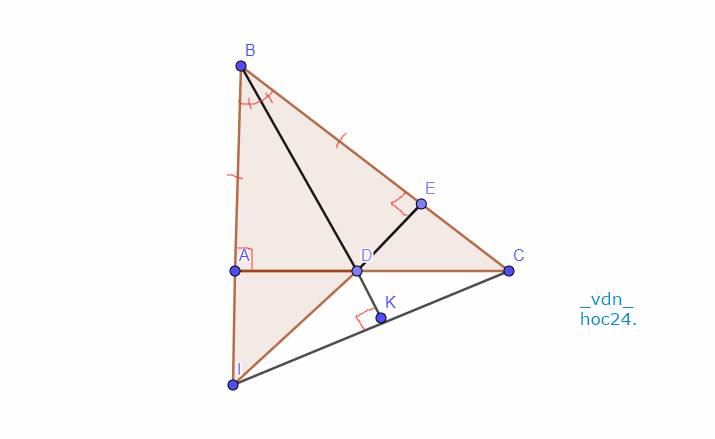
a: Xét ΔBAD và ΔBED có

BA=BE

góc ABD=góc EBD

BD chung

=>ΔBAD=ΔBED

b: ΔBAD=ΔBED

=>góc BED=90 độ

c: Xet ΔDAI vuông tại A và ΔDEC vuông tại E co

DA=DE
góc ADI=góc EDC

=>ΔDAI=ΔDEC

=>DI=DC và AI=EC

=>BI=BC

=>BD là trung trực của IC

=>BD vuông góc IC

Answer 2

\(\text{#TN}\)

`a,` Xét Tam giác `BAD` và Tam giác `BED` có:

`BA = BE (g``t)`

\(\widehat{ABD}=\widehat{EBD} (\text {tia phân giác}\)\(\widehat{BAE})\)

`\text {BD chung}`

`=> \text {Tam giác BAD = Tam giác BED (c-g-c)}`

`b,`

Vì Tam giác `BAD =` Tam giác `BED (a)`

`->`\(\widehat{BAD}=\widehat{BED} (\text {2 góc tương ứng})\)

Mà \(\widehat{BAD}=90^0\)

`->`\(\widehat{BAD}=\widehat{BED}=90^0\)

`->`\(\widehat{BED}\) \(\text { là góc vuông}\)

`c,`

Xét Tam giác `BAC` và Tam giác `BEI` có:

\(\widehat{B}\) \(\text {chung}\)

`BA = BE (g``t)`

\(\widehat{BAC}=\widehat{BEI}=90^0\)

`=> \text {Tam giác BAC = Tam giác BEI (g-c-g)}`

`-> BI = BC (\text {2 cạnh tương ứng})`

Gọi `K` là giao điểm của `BD` và `IC`

Xét Tam giác `BIK` và Tam giác `BCK` có:

`BI = BC (CMT)`

\(\widehat{KBC}=\widehat{KBI} (\text {tia phân giác}\) \(\widehat{IBC})\)

`\text {BK chung}`

`=> \text {Tam giác BIK = Tam giác BCK (c-g-c)}`

`->`\(\widehat{BKI}=\widehat{BKC} (\text {2 góc tương ứng})\)

Mà `2` góc này nằm ở vị trí kề bù

`->`\(\widehat{BKI}+\widehat{BKC}=180^0\)

`->`\(\widehat{BKI}=\widehat{BKC}=\) `180/2=90^0`

`-> \text {BK}` `\bot` `\text {IC}`

`-> \text {BD}` `\bot` `\text {IC (đpcm)}`