Các câu hỏi tương tự
Cho tam giác vuông cân ABC có
A
B
A
C
a
2
và hình chữ nhật MNPQ với MQ2MN được xếp chồng lên nhau sao cho M, N lần lượt là trung điểm của AB, AC (như hình vẽ). Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục AI, với I là trung điểm PQ.
Đọc tiếp
Cho tam giác vuông cân ABC có A B = A C = a 2 và hình chữ nhật MNPQ với MQ=2MN được xếp chồng lên nhau sao cho M, N lần lượt là trung điểm của AB, AC (như hình vẽ). Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục AI, với I là trung điểm PQ.
![]()
![]()
![]()
Cho nửa đường tròn đường kính AB 2R và điểm C thay đổi trên nửa đường tròn đó, đặt
α
C
A
B
⏞
và gọi H là hình chiếu vuông góc của C lên AB . Tìm
α
sao cho thể tích vật thể tròn xoay tạo thành khi quay tam giác ACH quanh trục AB đạt giá trị lớn nhất.
Đọc tiếp
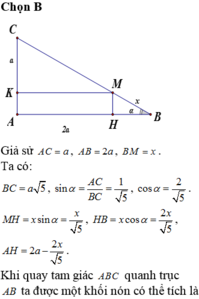
Cho nửa đường tròn đường kính AB = 2R và điểm C thay đổi trên nửa đường tròn đó, đặt α = C A B ⏞ và gọi H là hình chiếu vuông góc của C lên AB . Tìm α sao cho thể tích vật thể tròn xoay tạo thành khi quay tam giác ACH quanh trục AB đạt giá trị lớn nhất.
![]()
![]()
![]()
![]()
Cho nửa đường tròn đường kính AB2R và điểm C thay đổi trên nửa đường tròn đó, đặt
α
C
A
B
^
và gọi H là hình chiếu vuông góc của C lên AB. Tìm
α
sao cho thể tích vật thể tròn xoay tạo thành khi quay tam giác ACH quanh trục AB đạt giá trị lớn nhất.
Đọc tiếp
Cho nửa đường tròn đường kính AB=2R và điểm C thay đổi trên nửa đường tròn đó, đặt α = C A B ^ và gọi H là hình chiếu vuông góc của C lên AB. Tìm α sao cho thể tích vật thể tròn xoay tạo thành khi quay tam giác ACH quanh trục AB đạt giá trị lớn nhất.
![]()
![]()
![]()
![]()
Cho hình vuông ABCD có cạnh bằng 1m. Gọi M là trung điểm của AB, N thuộc cạnh BC thỏa mãn NC2NB. Gọi V là thể tích khối tròn xoay khi quay đa giác ADCNM quanh trục BC. Tính V.
Đọc tiếp
Cho hình vuông ABCD có cạnh bằng 1m. Gọi M là trung điểm của AB, N thuộc cạnh BC thỏa mãn NC=2NB. Gọi V là thể tích khối tròn xoay khi quay đa giác ADCNM quanh trục BC. Tính V.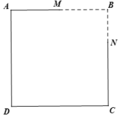
![]()
![]()
![]()
![]()
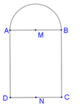
Cho hình chữ nhật ABCD và nửa đường tròn đường kính AB như hình vẽ. Gọi M, N lần lượt là trung điểm của AB, CD. Biết AB 4,AD 7. Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục MN.
Đọc tiếp
Cho hình chữ nhật ABCD và nửa đường tròn đường kính AB như hình vẽ. Gọi M, N lần lượt là trung điểm của AB, CD. Biết AB = 4,AD = 7. Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục MN.
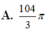
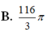
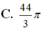
Cho hình chóp tam giác S. ABC có đáy ABC là tam giác đều cạnh a, SAa và SA vuông góc với mặt phẳng (ABC). Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Thể tích V của khối chóp A. BCNM bằng: A.
a
3
3
12
B.
a
3
3...
Đọc tiếp
Cho hình chóp tam giác S. ABC có đáy ABC là tam giác đều cạnh a, SA=a và SA vuông góc với mặt phẳng (ABC). Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Thể tích V của khối chóp A. BCNM bằng:
A. a 3 3 12
B. a 3 3 48
C. a 3 3 24
D. a 3 3 16
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, SA 2a và SA vuông góc với mặt phẳng (ABC). Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Thể tích V của khối chóp A.BCNM bằng A.
V
3
a
3
3
50
B.
V
9...
Đọc tiếp
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, SA = 2a và SA vuông góc với mặt phẳng (ABC). Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Thể tích V của khối chóp A.BCNM bằng
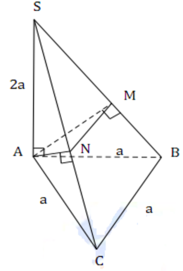
A. V = 3 a 3 3 50
B. V = 9 a 3 3 50
C. V = 8 a 3 3 75
D. V = 8 a 3 3 25
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, SA2a và SA vuông góc với mặt phẳng (ABC). Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Thể tích V của khối chóp A.BCNM bằng
Đọc tiếp
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, SA=2a và SA vuông góc với mặt phẳng (ABC). Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Thể tích V của khối chóp A.BCNM bằng
![]()
![]()
![]()
![]()
Cho đường tròn (C) có tâm I, bán kính
R
a
. Gọi M là điểm nằm ngoài (C) và
I
M
a
3
; A là điểm thuộc (C) và MA tiếp xúc với (C); H là hình chiếu của A trên đường thẳng IM. Tính theo a thể tích V của khối tròn xoay tạo bởi hình tam giác MAH quay xung quanh trục IM
Đọc tiếp
Cho đường tròn (C) có tâm I, bán kính R = a . Gọi M là điểm nằm ngoài (C) và I M = a 3 ; A là điểm thuộc (C) và MA tiếp xúc với (C); H là hình chiếu của A trên đường thẳng IM. Tính theo a thể tích V của khối tròn xoay tạo bởi hình tam giác MAH quay xung quanh trục IM
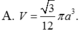
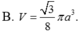
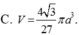
![]()