Các câu hỏi tương tự
cho tam giác abc vuông cân tại a, o là trung điểm cạnh bc. m là 1 điểm thuộc đoạn ob kẻ md,me vuông góc ab,ac. gọi m' là điểm đối xứng của m qua de. cm m'm là tia phân giác của b'mc
Cho tam giác ABC vuông cân tại A có M nằm giữa B và C sao cho BM < 1/2 BC. Kẻ MD, ME lần lượt vuông góc với AB, AC . Gọi N là điểm đối xứng của M qua đường thẳng DE. Chứng minh rằng:
Tứ giác ANDE là hình thang cân.NM là tia phân giác của góc BNC.
Cho tam giác ABC vuông tại A. Điểm M thuộc cạnh BC. Từ M vẽ các đường thẳng vuông góc với cạnh AB ở D và với cạnh AC ở E.a) Chứng minh AM DEb) Gọi I là điểm đối xứng của D qua A và K là điểm đối xứng của E qua M. Chứng minh rằng các đoạn thẳng IK, DE, AM đồng quy tại trung điểm O của mỗi đoạnc) Gọi AH là đường cao của tam giác ABC (H thuộc BC). Tính số đo góc DHEd) Tìm vị trí của điểm M trên cạnh BC để tứ giác DIEK là hình thoi
Đọc tiếp
Cho tam giác ABC vuông tại A. Điểm M thuộc cạnh BC. Từ M vẽ các đường thẳng vuông góc với cạnh AB ở D và với cạnh AC ở E.
a) Chứng minh AM = DE
b) Gọi I là điểm đối xứng của D qua A và K là điểm đối xứng của E qua M. Chứng minh rằng các đoạn thẳng IK, DE, AM đồng quy tại trung điểm O của mỗi đoạn
c) Gọi AH là đường cao của tam giác ABC (H thuộc BC). Tính số đo góc DHE
d) Tìm vị trí của điểm M trên cạnh BC để tứ giác DIEK là hình thoi
Cho tam giác ABC vuông tại A. Điểm M thuộc cạnh BC. Từ M vẽ các đường thẳng vuông góc với cạnh AB ở D và với cạnh AC ở E.a) Chứng minh AM DEb) Gọi I là điểm đối xứng của D qua A và K là điểm đối xứng của E qua M.Chứng minh rằng các đoạn thẳng IK, DE, AM đồng quy tại trung điểm O của mỗi đoạnc) Gọi AH là đường cao của tam giác ABC (H thuộc BC). Tính số đo góc DHEd) Tìm vị trí của điểm M trên cạnh BC để tứ giác DIEK là hình thoi
Đọc tiếp
Cho tam giác ABC vuông tại A. Điểm M thuộc cạnh BC. Từ M vẽ các đường thẳng vuông góc với cạnh AB ở D và với cạnh AC ở E.
a) Chứng minh AM = DE
b) Gọi I là điểm đối xứng của D qua A và K là điểm đối xứng của E qua M.Chứng minh rằng các đoạn thẳng IK, DE, AM đồng quy tại trung điểm O của mỗi đoạn
c) Gọi AH là đường cao của tam giác ABC (H thuộc BC). Tính số đo góc DHE
d) Tìm vị trí của điểm M trên cạnh BC để tứ giác DIEK là hình thoi
Cho tam giác ABC vuông tại A và M là trung điểm cạnh BC. Từ M kẻ MD vuông góc với AB (D thuộc AB) và ME vuông góc với AC (E thuộc AC)
a) Chứng minh tứ giác ADME là hình chữ nhật
b)Gọi N là điểm đối xứng với M qua E,O là giao điểm AM và DE.Chứng minh 3 điểm B,O,N thẳng hàng
c)Tam giác ABC cần điều kiện gì để tứ giác ABCN là hình thang cân
Cho tam giác ABC vuông tại A (AB AC) có đường cao AH. Kẻ HD vuông góc với AB (D thuộc AB), kẻ HE vuông góc với AC (E thuộc AC) a) Chứng minh tứ giác ADHE là hình chữ nhật. b) Gọi I là trung điểm của đoạn thẳng HC. Gọi K là điểm đối xứng với điểm A qua điểm I. Chứng minh rằng AC // HK. c) Chứng minh tứ giác DECK là hình thang cân. d) Gọi O là giao điểm của DE và AH; Gọi M là giao điểm của AI và CO. Chứng minh AM 1/3 AK
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC) có đường cao AH. Kẻ HD vuông góc với AB (D thuộc AB), kẻ HE vuông góc với AC (E thuộc AC) a) Chứng minh tứ giác ADHE là hình chữ nhật. b) Gọi I là trung điểm của đoạn thẳng HC. Gọi K là điểm đối xứng với điểm A qua điểm I. Chứng minh rằng AC // HK. c) Chứng minh tứ giác DECK là hình thang cân. d) Gọi O là giao điểm của DE và AH; Gọi M là giao điểm của AI và CO. Chứng minh AM = 1/3 AK
Cho tam giác ABC vuông tại A (AB AC) . M là trung điểm cạnh BC. Vẽ MD vuông góc với AB tại D và ME vuông góc với AC tại E.a) Chứng minh tứ giác ADME là hình chữ nhật.b) Chứng minh E là trung điểm của đoạn thẳng AC và tứ giác CMDE là hình bình hành.c) Vẽ đường cao AH của tam giác ABC. Chứng minh tứ giác MHDE là hình thang când) Qua A vẽ đường thẳng song song với DH cắt DE tại K. Chứng minh HK vuông góc với AC.
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC) . M là trung điểm cạnh BC. Vẽ MD vuông góc với AB tại D và ME vuông góc với AC tại E.
a) Chứng minh tứ giác ADME là hình chữ nhật.
b) Chứng minh E là trung điểm của đoạn thẳng AC và tứ giác CMDE là hình bình hành.
c) Vẽ đường cao AH của tam giác ABC. Chứng minh tứ giác MHDE là hình thang cân
d) Qua A vẽ đường thẳng song song với DH cắt DE tại K. Chứng minh HK vuông góc với AC.
Cho tam giác ABC vuông tại A, đường cao AH (H thuộc BC). Lấy M trên cạnh BC, kẻ MD vuông góc với AB, ME vuông góc với AC. Lấy I đối xứng với D qua A, K đối xứng với E qua M. Chứng minh:
a) Tứ giác ADME là hình gì?
b) Gọi O là giao điểm của AM và DE. Chứng minh: I; O; K thẳng hàng
c) Góc DHE = 90 độ
d) Tìm vị trí của M trên BC để tứ giác AEKB là hình chữ nhật
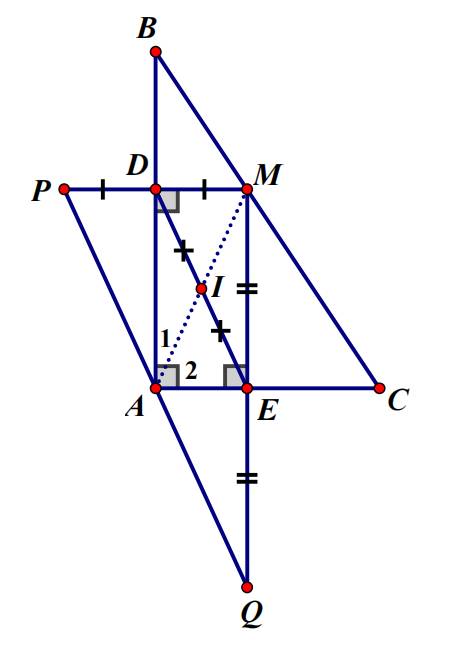
Bài 2: Cho △ABC vuông tại A. Lấy điểm M thuộc cạnh BC. Kẻ MD và ME lần lượt vuông góc với AB và AC ( D thuộc AB, E thuộc AC ). Lấy I là trung điểm của DE. a) Tứ giác ADME là hình gì? Vì sao? b) Chứng minh ba điểm A, I, M thẳng hàng. c) Trên tia đối của tia DM lấy điểm P, trên tia đối của tia EM lấy điểm Q sao cho, DPDM, EQEM Chứng minh A, P, Q thẳng hàng và A là trung điểm PQ
Đọc tiếp
Bài 2: Cho △ABC vuông tại A. Lấy điểm M thuộc cạnh BC. Kẻ MD và ME lần lượt vuông góc với AB và AC ( D thuộc AB, E thuộc AC ). Lấy I là trung điểm của DE.
a) Tứ giác ADME là hình gì? Vì sao?
b) Chứng minh ba điểm A, I, M thẳng hàng.
c) Trên tia đối của tia DM lấy điểm P, trên tia đối của tia EM lấy điểm Q sao cho, DP=DM, EQ=EM
Chứng minh A, P, Q thẳng hàng và A là trung điểm PQ