Các câu hỏi tương tự
Cho tam giác ABC vuông cân tại A, M là trung điểm BC. Lấy điểm D bất kì thuộc cạnh BC. H và I thứ tự là hình chiếu của B và C xuống đường thẳng AD. Đường thẳng AM cắt CI tại N. Chứng minh rằng:
a) BH = AI.
b) BH^2 + CI^2 = 2AM^2
c) IM là phân giác của góc HIC
Cho tam giác ABC vuông cân tại A, M là trung điểm của BC. Lấy điểm D bất kì thuộc cạnh BC. H và I thứ tự là hình chiếu của B và C xuống đường thẳng AD.Đường thẳng AM cắt CI tại N.CMR:
a) BH=AI
b) Đường thẳng DN vuông góc với AC
c) IM là tia phân giác của góc HIC
CÓ AI GIÚP EM PHẦN c VỚI NGHĨ MÃI KHÔNG RA
Cho tam giác ABC vuông cân tại A, M là trung điểm BC. Lấy điểm D bất kì thuộc cạnh BC. H và I thứ tự là hình chiếu của B và C xuống đường thẳng AD. Đường thẳng AM cắt CI tại N. Chứng minh rằng: a) BH AI. b) BH2 + CI2 có giá trị không đổi. c) Đường thẳng Dn vuông góc với AC.
Đọc tiếp
Cho tam giác ABC vuông cân tại A, M là trung điểm BC. Lấy điểm D bất kì
thuộc cạnh BC. H và I thứ tự là hình chiếu của B và C xuống đường thẳng AD. Đường
thẳng AM cắt CI tại N. Chứng minh rằng:
a) BH = AI.
b) BH2 + CI2 có giá trị không đổi.
c) Đường thẳng Dn vuông góc với AC.
Cho tam giác đều ABC có cạnh bằng a, trên đường thẳng
∆
đi qua A vuông góc với mặt phẳng (ABC) lấy điểm M bất kì. Gọi E, F lần lượt là hình chiếu vuông góc của B lên MC, AC và đường thẳng
∆
cắt EF tại N (như hình bên). Khi đó thể tích của tứ diện MNBC đạt giá trị nhỏ nhất bằng bao nhiêu? A.
a
3
6
4
....
Đọc tiếp
Cho tam giác đều ABC có cạnh bằng a, trên đường thẳng ∆ đi qua A vuông góc với mặt phẳng (ABC) lấy điểm M bất kì. Gọi E, F lần lượt là hình chiếu vuông góc của B lên MC, AC và đường thẳng ∆ cắt EF tại N (như hình bên). Khi đó thể tích của tứ diện MNBC đạt giá trị nhỏ nhất bằng bao nhiêu?
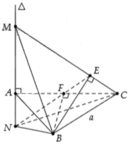
A. a 3 6 4 .
B. a 3 3 4 .
C. a 3 3 6 .
D. a 3 6 12 .
Trong mặt phẳng tọa độ Oxy, cho hình bình hành ABCD có diện tích bằng 16. Biết tam giác ABC cân tại A, cạnh BC4 và
K
(
21
5
;
18
5
)
là hình chiếu của điểm B xuống AC. Tìm tọa độ điểm D biết rằng điểm B thuộc đường thẳng
△
:
x
+
y
-
3
0
đồng thời hoành độ các điểm B, C đều là các số nguyên A....
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho hình bình hành ABCD có diện tích bằng 16. Biết tam giác ABC cân tại A, cạnh BC=4 và K ( 21 5 ; 18 5 ) là hình chiếu của điểm B xuống AC. Tìm tọa độ điểm D biết rằng điểm B thuộc đường thẳng △ : x + y - 3 = 0 đồng thời hoành độ các điểm B, C đều là các số nguyên
A. D(5;2)
B. D(7;6)
C. (-7;-6)
D. D(-5;-2)
Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh BC, trên tia đối của tia CB lấy điểm E sao cho CE=BD. Các đường thẳng vuông góc với BC tại D và E lần lượt cắt các đường thẳng AB và Ac theo thứ tự tại M, N. Gọi I là giao điểm của MN với BC. CMR đường thẳng vuông góc với MN luôn đi qua một điểm cố đinh.
Cho tam giác ABC vuông tại A có AB= 9cm ; BC=10cm
a. Tính AC và so sánh các góc tam giác ABC
b. Trên tia đối tia AB lấy điểm D sao cho A là trung điểm BD. Chứng minh tam giác BCD cân
c. Gọi E; F lần lượt là trung điểm các cạnh DC, BC. Đường thẳng BE cắt cạnh AC tại M.
Tính CM và chứng minh 3 điểm D; M; F thẳng hàng
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho HA2HB. Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60°. Tính khoảng cách d giữa hai đường thẳng SA và BC theo a. A.
d
a
42
8
B.
d
a
21...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho HA=2HB. Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60°. Tính khoảng cách d giữa hai đường thẳng SA và BC theo a.
A. d = a 42 8
B. d = a 21 12
C. d = a 42 12
D. d = a 462 66
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho
H
A
2
H
B
. Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60°. Tính khoảng cách d giữa hai đường thẳng SA và BC theo a. A.
d
a
42
8
B.
d
a
21...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho H A = 2 H B . Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60°. Tính khoảng cách d giữa hai đường thẳng SA và BC theo a.
A. d = a 42 8
B. d = a 21 12
C. d = a 42 12
D. d = a 462 66







