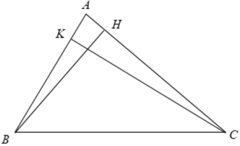
Xét Δ ABH và Δ ACK có
⇒ Δ ABH ∼ Δ ACK ( g - g )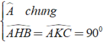

Xét Δ ABH và Δ ACK có
⇒ Δ ABH ∼ Δ ACK ( g - g )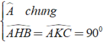
Cho tam giác ABC và các đường cao BH, CK. Chứng minh Δ ABH ∼ Δ ACK.
cho tam giác abc và các đường cao BH,CK
a) chứng minh tam giác ABH đồng dạng với tam giác ACK
b)Cho góc ACB= 40, Tính góc AKH
cho tam giác nhọn ABC có BH và CK thứ tự là các đường cao ứng cạnh AC và AB. lấy ddieemr M thuộc tia đói của tia BH sao cho BM = AC . Lấy điểm N thuộc tia đối của tia CK sao cho CN = CB
a) chứng minh rằng góc ABH = góc ACK
Cho Δ ABC cân tại A vẽ các đường cao BH và CK. Chứng minh
a) BK=CH
b) KH//BC
Cho Δ ABC vuông tại A có AH là đường cao ( H thuộc cạnh BC ) . Biết AB = 21cm , AC = 28cm . a) Tính độ dài các Cạnh BC , BH . b) Chứng minh : Δ ABH đồng dạng Δ CBA
Cho Δ nhọn ABC, có BD \(\perp\) AC và CE \(\perp\) AB , Mlà trung điểm BC . Chứng minh:
a) Δ MED cân
b)Vẽ BH,CK⊥DE. chứng minh EH= DK
Cho tam giác ABC vuông tại A có đường cao AH
a/ Chứng minh tam giác ABH đồng dạng tam giác CBA.
b/ Gọi M là trung điểm của BH. Kẻ CK vuông góc với AM tại K , CK cắt AH tại I. Chứng minh IA = IH
Cho tam giác ABC có ba góc nhọn và AB < AC. Vẽ hai đường cao BD và CE.
a) Chứng minh: ΔABD đồng dạng ΔACE . Suy ra : AB.AE = CA. AD
b) Chứng minh: Δ ADE đồng dạng Δ ABC .
c) Tia DE và CB cắt nhau tại I. Chứng minh: Δ IBE đồng dạng Δ IDC .
d) Gọi O là trung điểm BC. Chứng minh ID.IE= OI^2 - OC^2
Cho tam giác ABC có ba góc nhọn và AB < AC. Vẽ hai đường cao BD và CE.
a) Chứng minh: ΔABD đồng dạng ΔACE . Suy ra : AB.AE = CA. AD
b) Chứng minh: Δ ADE đồng dạng Δ ABC .
c) Tia DE và CB cắt nhau tại I. Chứng minh: Δ IBE đồng dạng Δ IDC .
d) Gọi O là trung điểm BC. Chứng minh ID.IE= OI^2 - OC^2