Xét tứ giác AMHN có: A M H ^ + A N H ^ = 90 0 + 90 0 = 180 0 => Đpcm
Xét tứ giác BNMC có: B N C ^ = B M C ^ = 90 0 => Đpcm
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
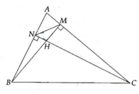
Cho tam giác nhọn ABC có đường cao BM và CN cắt nhau tại H. CM tứ giác AMHN và BNMC nội tiếp .
cho tam giác abc nhọn nội tiếp đường tròn tâm o bán kính R, hai đường cao BM và CN cắt nhau tại H.
a) chứng minh tứ giác BNMC nội tiếp. xác định tâm I của đường tròn ngooaij tiếp tứ giác này
b) chứng minh tam giác AMN đồng dạng tam giác ABC
c) chứng minh OI // AH
d) E là giao điểm của AH và BC, chứng minh MH là phân giác của góc NME
P/s: mình cần câu d thôi ạ
cho tam giác ABC nội tiếp đường tròn tâm O bán kính bằng 5cm, hai đường cao BM và CN cắt nhau tại H.
a, Chứng minh tứ giác AMHN nội tiếp
b, chứng minh tứ giác BNMC nội tiếp
c, chứng minh OA vuông góc với MN
Mọi người giải chi tiết giúp mình với nhé !! Cảm Ơn
Cho tam giác ABC nhọn nội tiếp (O) vẽ 2 đường cao BM và CN cắt nhau tại H
a/ Chứng minh AH vuông góc BC
b/ Chứng minh tứ giác AMHN nội tiếp
c/ Chứng minh BCMN thuộc đường tròn xác định tâm I
d/ Vẽ tiếp tuyến Ax. Chứng minh OA vuông góc MN
cho tam giác ABC nhọn nội tiếp đường tròn (O), hai đường cao BM,CN của tam giác ABC cắt nhau tại H . chứng minh:
a. tứ giác BCMN nội tiếp. xác định tâm E của đường tròn ngoại tiếp tứ giác BCMN
b. tam giác AMN đồng dạng tam giác ABC
c. tia AO cắt đường tròn (O) tại K, cắt MN tại I . chứng minh: tứ giác BHCK là hình bình hành
d. chứng minh: AK vuông góc MN
Cho tam giác ABC có ba góc nhọn nội tiếp (O,R). Hai đường cao AN và BM của tam giác ABC cắt nhau tại I
a Chứng minh tứ giác IMCN nội tiếp được một đường tròn
b chứng minh IA.IN=IM.IB
c tia BM cắt (O) tại H Chứng minh AI=AH
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O). Hai đường cao AD và CE cắt nhau tại H. Tia BO cắt (O) tại điểm thứ hai M. I là giao điểm của BM và DE
a) Chứng minh tứ giác AEDC là tứ giác nội tiếp
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O). Hai đường cao AD và CE cắt nhau tại H. Tia BO cắt (O) tại điểm thứ hai M. I là giao điểm của BM và DE
c) Chứng minh tứ giác CMID là tứ giác nội tiếp
Cho tam giác ABC có ba góc nhọn nội tiếp (O;R). Hai đường cao AN và BM của tam giác ABC cắt nhau tại I a) Chứng minh tứ giác IMCN nội tiêpa một đường tròn b) Chứng minh: IA.IN=IB.IM c) Tia BM cắt (O) tại H. Chứng minh AI = AH