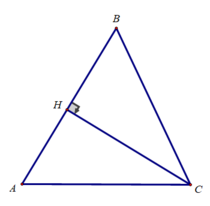
Kẻ đường cao CH của tam giác ABC. Ta có:
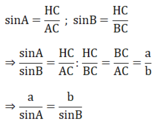
Chứng minh tương tự ta có:
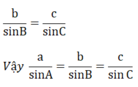

Kẻ đường cao CH của tam giác ABC. Ta có:
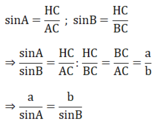
Chứng minh tương tự ta có:
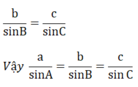
Cho tam giác nhọn ABC. Gọi a, b, c lần lượt là độ dài các cạnh đối diện với các đỉnh A, B, C. Chứng minh rằng: a/ sin A= b/ sin B= c/ sinC
Cho tam giác nhọn ABC . gọi a,b,c lần lượt là đọ dài các cạnh đối diện với đỉnh ABC . CMR a / sin A = b / sin B = c / sin C.
cho a, b, c lần lượt là độ dai cạnh BC, AC, AB của tam giác ABC.
a) chứng minh rằng \(\sin\frac{A}{2}\le\frac{a}{2\sqrt{bc}}\)
b) chưng minh rằng \(\sin\frac{A}{2}.\sin\frac{B}{2}.\sin\frac{C}{2}\le\frac{1}{8}\)
c)đường cao AD, BE cắt nhau ở H. chứng minh \(AD.HD\le\frac{BC^2}{4}\)
Cho tam giác ABC nhọn với AB = c , AC = b , BC = a . Chứng minh :
\(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\)
cho tam giác ABC nhọn, BC=a, AC=b, AB=c
chứng minh:
\(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\)
Cho tam giác ABC có a, b, c là độ dài các cạnh BC, AC, Ab. Chứng minh rằng: sin \(\frac{A}{2}\)< hoặc = \(\frac{a}{b+c}\)
Cho tam giác ABC biết AB=12cm , AC=9cm , BC=15cm.
a. Chứng minh tam giác ABC vuông
b. Tính; \(\frac{\sin B+\sin C}{\sin B-\sin C}\)
c. Tính độ dài đường cao AH
d. Gọi M và N lần lượt là hình chiếu của H trên AB và AC. Chứng minh \(AM\cdot AB=AN\cdot AC\)
e. Chứng minh \(AH=\frac{BC}{\cot B+\cot C}\)
f. Chứng minh \(S_{AMN}=\sin^2B\cdot\sin^2C\cdot S_{ABC}\)
Giúp mk nhanh nhé mn ơi
Cho tam giác ABC nhọn có BC=a, AC=b, AB=c
Chứng minh
\(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\)
Cho tam giác ABC nhọn và BC = a , CA = b , AB = c
CM:\(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\)