Các câu hỏi tương tự
Cho tam giác ABC nhọn AB<AC nội tiếp (O). 3 đường cao AD,BE,CF của tam giác ABC cắt nhau tại H. Đường thẳng EF cắt (O) tại M và N ( M thuộc cung nhỏ AB ) . Gọi I là trung điểm của BC , MI cắt (O) tại K . Chứng minh : AK vuông góc với HN
cho tam giác ABC nhọn nội tiếp đường tròn(O;R)biết AB<AC ,các đường cao AD,BE,CF cắt nhau tại H.Gọi I là trung điểm BC ,kẻ tiếp tuyến Ax với (O),A là tiếp điểm
!,C/m:tứ giác BEFC,FDIE nội tiếp
2,C/m:OA vuông góc EF
Câu 4(3,0 điểm) Cho tam giác ABC có ba góc nhọn (AB < AC), nội tiếp đường tròn tâm O. Các đường cao AD, BE, CF của tam giác ABC cắt nhau tại H. Gọi M là giao điểm của EF và BC. Qua B kẻ đường thẳng song song với AC cắt AM tại P và AD tại Q.
a) Chứng minh tứ giác AEHF nội tiếp.
b) Chứng minh DFC = EFC.
c) Chứng minh BP = BQ.
Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O), các đường cao AD, BE và CF cắt nhau tại H.
a) Chứng minh tứ giác AEHF và BCEF nội tiếp.
b) Hai đường thẳng EF và BC cắt nhau tại M. Chứng minh MB.MC = ME.MF.
c) AM cắt đường tròn (O) tại N. Đường thẳng qua B và song song với AC cắt AM tại I và cắt AH tại K. Chứng minh AN vuông góc HN và HI = HK.
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn O(AB<AC) có 3 đường cao AD,BE,CF cắt nhau tại H. EF cắt BC tại M và cắt AD tại I, AM cắt (O) tại N. Chứng minh NI là phân giác của góc END.
Cho tam giác ABC nhọn ( AB AC ) nội tiếp (O) . Gọi H là giao điểm ba đườngcao AD BE CF , , và đường thẳng EF cắt BC tại M . Đường thẳng MA cắt (O) tại K .a) Chứng minh: Tứ giác BCEF và tứ giác MBFK nội tiếp.b) Chứng minh: 5 điểm A K F H E , , , , cùng thuộc một đường tròn.c) Tia KH cắt (O) tại N . Chứng minh. .2.ABCAB AC BCANS
Đọc tiếp
Cho tam giác ABC nhọn ( AB AC ) nội tiếp (O) . Gọi H là giao điểm ba đường
cao AD BE CF , , và đường thẳng EF cắt BC tại M . Đường thẳng MA cắt (O) tại K .
a) Chứng minh: Tứ giác BCEF và tứ giác MBFK nội tiếp.
b) Chứng minh: 5 điểm A K F H E , , , , cùng thuộc một đường tròn.
c) Tia KH cắt (O) tại N . Chứng minh
=
. .
2.
ABC
AB AC BC
AN
S
cho tam giác ABC có 3 góc nhọn (AB<AC) nội tiếp đường tròn tâm O. Vẽ đường cao AD,BE,CF cắt nhau tại H
a) CM AFHE và BFEC là tứ giác nội tiếp
b) dường thẳng EF cắt BC tại I.CM IE.IF=IB.IC
c) AI cắt đường tròn tâm O tại K. M là trung điểm BC.CM 3 điểm K,H,M thẳng hàng
Cho tam giác ABC nhọn nội tiếp đường tròn tâm O bán kính R(ABAC),3 đường cao AD,BE,CF cắt nhau tại H.Vẽ Ak là đường kính của đường tròn tâm O.Tia EF cắt đường tròn tại I.Gọi G là gaio điểm của BC và IK.a)Cm:BCEF nội tiếp và ADGI nội tiếpb)Tiếp tuyến tại B của đường (o,R) cắt EF tại T.Vẽ Om vuông góc BC tại m.Chứng minh TM song song CF và tú giác TBME nội tiếpc)Tia Mh cắt đường tròn tâm O tại N,AN cắt È tại V.Chứng minh V,B,C thẳng hàngd)chứng minh:HI vuông góc Ag
Đọc tiếp
Cho tam giác ABC nhọn nội tiếp đường tròn tâm O bán kính R(AB<AC),3 đường cao AD,BE,CF cắt nhau tại H.Vẽ Ak là đường kính của đường tròn tâm O.Tia EF cắt đường tròn tại I.Gọi G là gaio điểm của BC và IK.
a)Cm:BCEF nội tiếp và ADGI nội tiếp
b)Tiếp tuyến tại B của đường (o,R) cắt EF tại T.Vẽ Om vuông góc BC tại m.Chứng minh TM song song CF và tú giác TBME nội tiếp
c)Tia Mh cắt đường tròn tâm O tại N,AN cắt È tại V.Chứng minh V,B,C thẳng hàng
d)chứng minh:HI vuông góc Ag
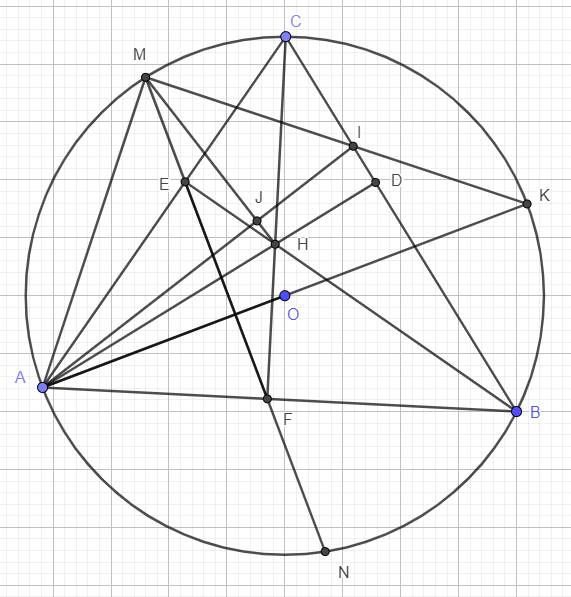
Cho tam giác ABC nối tiếp (O), có ba đường cao AD, BE, CF cắt nhau tại H. Đường thẳng EF cắt hai cung nhỏ AB, AC tại N, M. Vẽ đường kính AK của (O), I là giao điểm của MK với BC, chứng minh AI vuông góc với HM
Cho tam giác ABC nhọn, AB > AC nội tiếp (O). Đường cao BE, CF cắt nhau tại H. AO cắt EF tại I, cắt (O) tại J.
a, CMR : BFIJ nội tiếp
b, BC cắt EF tại M, N : giao của AM với (O). CMR : ANEF nội tiếp.










