Question

Cho tam giác ABC nhọn (AB < AC), có 3 đường cao AD,BE,CF cắt nhau tại H:

a) Chứng minh tam giác HBE đồng dạng với tam giác HEC

b) Chứng minh BH.BE=BD.BC

 

Answer 1

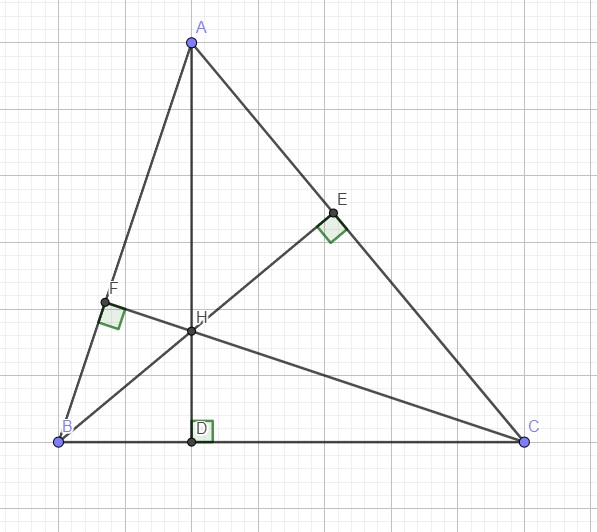
Câu a chắc em ghi đề nhầm, H,B,E thẳng hàng nên làm sao nó là tam giác được.

HFB và HEC đồng dạng thì đúng

Answer 2

a.

Do BE, CF là các đường cao \(\Rightarrow\widehat{BFH}=\widehat{CEH}=90^0\)

Xét hai tam giác HFB và HEC có:

\(\left\{{}\begin{matrix}\widehat{BFH}=\widehat{CEH}=90^0\\\widehat{BHF}=\widehat{CHE}\left(\text{đối đỉnh}\right)\end{matrix}\right.\) 

\(\Rightarrow\Delta HFB\sim\Delta HEC\left(g.g\right)\)

b.

Do AD là đường cao ứng với BC và H thuộc AD \(\Rightarrow\widehat{BDH}=90^0\)

Xét hai tam giác BDH và BEC có:

\(\left\{{}\begin{matrix}\widehat{BDH}=\widehat{BEC}=90^0\\\widehat{DBH}-chung\end{matrix}\right.\)

\(\Rightarrow\Delta BDH\sim\Delta BEC\left(g.g\right)\)

\(\Rightarrow\dfrac{BH}{BC}=\dfrac{BD}{BE}\Rightarrow BH.BE-BD.BC\)

Answer 3