Áp dụng định lí sin trong tam giác: a sin A = b sin B = c sin C = 2 R
Suy ra: b = 2R sin B; c = 2R . sin C
Ta có, S = 1 2 a . h a nên :
h a = 2 S a = 2 a b c 4 R a = b c 2 R = 2 R s i n B .2 R s i n C 2 R = 2 R s i n B s i n C
ĐÁP ÁN C
Áp dụng định lí sin trong tam giác: a sin A = b sin B = c sin C = 2 R
Suy ra: b = 2R sin B; c = 2R . sin C
Ta có, S = 1 2 a . h a nên :
h a = 2 S a = 2 a b c 4 R a = b c 2 R = 2 R s i n B .2 R s i n C 2 R = 2 R s i n B s i n C
ĐÁP ÁN C
Cho các khẳng định sau: (I): \(N\cap Z=N\) (II): R\Q = Z (III): Q \(\cup R=R\) (IV): \(Q\cup N\)* = N*
Trong các khẳng định sau có bao nhiêu khẳng định là mệnh đề đúng?
Bài 4 : ( 3,5 điểm) Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O; R) (với AB < AC). BE và CF là 2 đường cao của tam giác cắt nhau tại H
a) Chứng minh tứ giác BEFC và AEHF là tứ giác nội tiếp
b) Đường thẳng EF cắt đường thẳng BC tại S và EF cắt đường tròn (O) tại M và N (M nằm giữa S và E). Chứng minh SM. SN = SE. SF
c) Tia CE cắt đường tròn (O) tại K, vẽ dây KI song song với EF.
Chứng minh H, K đối xứng nhau qua AB
d) Chứng minh 3 điểm H, F, I thẳng hàng.
Bài 10:Cho ABC có a = 8, b =10, c =13 a. ABC có góc tù hay không ? Tính bán kính đường tròn ngoại tiếp ABC. b. Tính diện tích ABC
Bài 11:Cho tam giác ABC có: a = 6, b = 7, c = 5. a) Tính S ,h ,R,r ABC a b) Tính bán kính đường tròn đi qua A, C và trung điểm M của cạnh AB.
Bài 12:Cho tam giác ABC có: AB = 6, BC = 7, AC = 8. M trên cạnh AB sao cho MA = 2 MB. a) Tính các góc của tam giác ABC. b) Tính S ,h ,R ABC a , r. c) Tính bán kính đường tròn ngoại tiếp ∆MBC.
Bài 13:Cho ABC có 0 0 A B b = = = 60 , 45 , 2 tính độ dài cạnh a, c, bán kính đường tròn ngoại tiếp và diện tích tam giác ABC
Bài 14:Cho ABC AC = 7, AB = 5 và 3 cos 5 A = . Tính BC, S, a h , R, r.
Bài 15:Cho ABC có 4, 2 m m b c = = và a =3 tính độ dài cạnh AB, AC.
Bài 16:Cho ABC có AB = 3, AC = 4 và diện tích S = 3 3 . Tính cạnh BC
Bài 17:Cho tam giác ABC có ˆ o A 60 = , c h 2 3 = , R = 6. a) Tính độ dài các cạnh của ∆ABC. b) Họi H là trực tâm tam giác ABC. Tính bán kính đường tròn ngoại tiếp ∆AHC.
Bài 18:a. Cho ABC biết 0 0 a B C = = = 40,6; 36 20', 73 . Tính BAC , cạnh b,c. b.Cho ABC biết a m = 42,4 ; b m = 36,6 ; 0 C = 33 10' . Tính AB, và cạnh c.
Bài 19:Tính bán kính đường tròn nội tiếp ABC biết AB = 2, AC = 3, BC = 4.
Bài 20:Cho ABC biết A B C (4 3; 1 , 0;3 , 8 3;3 − ) ( ) ( ) a. Tính các cạnh và các góc của ABC b. Tính chu vi và diện tích ABC
1. Cho tam giác ABC có a \(=4\sqrt{2}\), c \(=10\), B\(=45^0\). Tính b, cos C, S, R, sin A, ha
Bài 4 : ( 3,5 điểm)
1) Cho đường tròn (O; R) và dây BC cố định, BC= R√3 A là điểm di động trên cung lớn BC (A khác B, C) sao cho tam giác ABC nhọn. Các đường cao BD và CE của tam giác ABC cắt nhau tại điểm H. Kẻ đường kính AF của đường tròn (O), AF cắt BC tại điểm N.
a) Chứng minh tứ giác BEDC là tứ giác nội tiếp
b) Chứng minh AE.AB = AD.AC
c) Gọi I là trung điểm của BC
Chứng minh rằng F, I, H thẳng hàng
2) Một hình trụ có diện tích xung quanh bằng 128π cm2, chiều cao bằng bán kính đáy. Tính thể tích của hình trụ đó
Gọi S = \(m^2_a+m^2_b+m^2_c\) là tổng bình phương độ dài ba trung tuyến của tam giác ABC. Trong các mệnh đề sau mệnh đề nào đúng?
A. S = \(\dfrac{3}{4}\left(a^2+b^2+c^2\right)\)
B. S = \(a^2+b^2+c^2\)
D. S = 3\(\left(a^2+b^2+c^2\right)\)
C. S = \(\dfrac{3}{2}\left(a^2+b^2+c^2\right)\)
Bài 4. (0,5 điểm) Từ hai vị trí $A$ và $B$ của một tòa nhà, người ta quan sát đỉnh $C$ của ngọn núi.
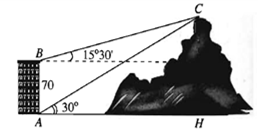
Biết rằng độ cao $AB=70$ m, phương nhìn $AC$ tạo với phương nằm ngang góc ${{30}^{\circ}}$, phương nhìn $BC$ tạo với phương nằm ngang góc ${{15}^{\circ}}30'$ (tham khảo hình vẽ trên). Ngọn núi đó có độ cao so với mặt đất là bao nhiêu mét?
1. Cho tam giác ABC có a =4√2, c =10, B=450. Tính b, cos C, S, R, sin A, ha
MN GIÚP E BÀI NÀY VỚI Ạ. E ĐANG CẦN GẤP LẮM Ạ.
1. Cho tam giác ABC có a =4√2=42, c =10=, B=450. Tính b, cos C, S, R, sin A, ha
MN GIÚP E BÀI NÀY VỚI Ạ. E ĐANG CẦN GẤP LẮM Ạ.
1. Cho tam giác ABC có a =\(4\sqrt{2}\), c =10, B=450. Tính b, cos C, S, R, sin A, ha
MN GIÚP E BÀI NÀY VỚI Ạ. E ĐANG CẦN GẤP LẮM Ạ.