a)các vectow cùng phương với AM LÀ: MA ;MB;BM;BA;AB;PN;NP
b)các vectow cùng hướng MN là:BP;PC;BC
c)các vectow ngược hướng với BC là:CP;CP;NM
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho tam giác đều ABC . Gọi M,N ,P lần lượt là các điểm thoả mãn vectơ BM = k vectơ BC , 4 vectơ AN = 3 vectơ AB , 3 vectơ AP = 2 vectơ AC . a, Biểu diễn vectơ AM theo hai vectơ AB , AC . b, Tìm k để hai đường thẳng AM , NP vuông góc với nhau.
Cho tam giác ABC, gọi M, N, P lần lượt là trung điểm các cạnh BC, CA, AB. Số vectơ bằng vectơ M N → có điểm đầu và điểm cuối trùng với một trong các điểm A, B, C, M, N, P bằng:
A. 1
B. 2
C. 3
D. 6
Cho M; N; P lần lượt là trung điểm các cạnh AB; BC; CA của tam giác ABC Hỏi vectơ
M
P
→
+
N
P
→
bằng vectơ nào?
Đọc tiếp
Cho M; N; P lần lượt là trung điểm các cạnh AB; BC; CA của tam giác ABC Hỏi vectơ M P → + N P → bằng vectơ nào?
Cho tam giác ABC. Các điểm M, N và P lần lượt là trung điểm của các cạnh AB, AC và BC.Tổng nào sau đây khác vectơ
0
→
? A.
A
M
→
+
B
P
→
+
C
N
→
B.
B...
Đọc tiếp
Cho tam giác ABC. Các điểm M, N và P lần lượt là trung điểm của các cạnh AB, AC và BC.
Tổng nào sau đây khác vectơ 0 → ?
A. A M → + B P → + C N →
B. B M → + A N → + C P →
C. A M → + B M → + C M →
D. A M → + A N → - A P →
Cho tứ giác ABCD. Trên cạnh AB; CD lấy lần lượt các điểm M, N sao cho
3
A
M
→
2
A
B
→
và
3
D
N
→
2
D
C
→
.
Tính vectơ
M
N
→
theo hai ve...
Đọc tiếp
Cho tứ giác ABCD. Trên cạnh AB; CD lấy lần lượt các điểm M, N sao cho 3 A M → = 2 A B → và 3 D N → = 2 D C → . Tính vectơ M N → theo hai vectơ A D → , B C → .
A. M N → = 1 3 A D → + 1 3 B C → .
B. M N → = 1 3 A D → − 2 3 B C → .
C. M N → = 1 3 A D → + 2 3 B C → .
D. M N → = 2 3 A D → + 1 3 B C → .
Cho tứ giác ABCD. Trên cạnh AB; CD lấy lần lượt các điểm M; N sao cho
3
A
M
→
2
A
B
→
và
3
D
N
→
2
D
C
→
.
Tính vectơ
M
N
→
theo hai ve...
Đọc tiếp
Cho tứ giác ABCD. Trên cạnh AB; CD lấy lần lượt các điểm M; N sao cho 3 A M → = 2 A B → và 3 D N → = 2 D C → . Tính vectơ M N → theo hai vectơ A D → , B C → .
A. M N → = 1 3 A D → + 1 3 B C → .
B. M N → = 1 3 A D → − 2 3 B C → .
C. M N → = 1 3 A D → + 2 3 B C → .
D. M N → = 2 3 A D → + 1 3 B C → .
Trên đường thẳng chứa cạnh BC của tam giác ABC lấy điểm M sao cho
M
B
→
1
3
M
C
→
. Khi đó vectơ
A
M
→
biểu diễn theo các vectơ
u
→
A
B
→
;
v...
Đọc tiếp
Trên đường thẳng chứa cạnh BC của tam giác ABC lấy điểm M sao cho M B → = 1 3 M C → . Khi đó vectơ A M → biểu diễn theo các vectơ u → = A B → ; v → = A C → là
A. A M → = 3 2 u → - 1 2 v →
B. A M → = 3 2 v → + 1 2 u →
C. A M → = - 3 2 v → - 1 2 u →
D. A M → = - 3 2 v → + 1 2 u →
Cho hai vectơ a và b đều khác vectơ 0. Các khẳng định sau đúng hay sai?a, Hai vecto cùng hướng thì cùng phương.b, Hai vecto b→ và kb→ cùng phương.c, Hai vecto a→ và (-2)a→ cùng hướng.d) Hai vector ngược hướng với vector thứ ba khác vectơ 0→ thì cùng phương.
Đọc tiếp
Cho hai vectơ a và b đều khác vectơ 0. Các khẳng định sau đúng hay sai?
a, Hai vecto cùng hướng thì cùng phương.
b, Hai vecto b→ và kb→ cùng phương.
c, Hai vecto a→ và (-2)a→ cùng hướng.
d) Hai vector ngược hướng với vector thứ ba khác vectơ 0→ thì cùng phương.
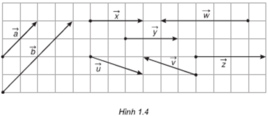
Trong hình 1.4, hãy chỉ ra các vectơ cùng phương, cùng hướng, ngược hướng và các vectơ bằng nhau.
