Các câu hỏi tương tự
Cho tam giác ABC. Gọi I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Qua I kẻ đường thẳng song song với BC cắt AB, AC lần lượt tại E và F. Chứng minh rằng EF = BE + CF.
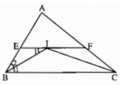
Cho tam giac ABC. Gọi I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó .Qua Ikẻ đương thẳng song song với BC cắt AB, AC lần lượt tại Evà F.Chứng minh EF=BE+CF
Cho tam giác ABC, đường phân giác của góc B và đường phân giác của C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC cắt AB, AC lần lượt tại E, F.a) Chứng mình BEI, CFI là các tam giác cân.b) Chứng minh BE + CF EF.c) Gọi M là trung điểm của IB, N là trung điểm của IC, các đường thẳng EM, FN cắt nhau tại O. Chứng minh OB OC.d) Chứng minh ba điểm A, I, O thẳng hàng.
Đọc tiếp
Cho tam giác ABC, đường phân giác của góc B và đường phân giác của C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC cắt AB, AC lần lượt tại E, F.
a) Chứng mình BEI, CFI là các tam giác cân.
b) Chứng minh BE + CF = EF.
c) Gọi M là trung điểm của IB, N là trung điểm của IC, các đường thẳng EM, FN cắt nhau tại O. Chứng minh OB = OC.
d) Chứng minh ba điểm A, I, O thẳng hàng.
Cho tam gác abc có góc a75 độ, góc c35 độ, m là trung điểm của bc. đường thẳng đi qua m và vuông góc với phân giác của góc a cắt ab, ac lần lượt tại e và fa/ chứng minh rằng: becfb/ đường thẳng qua e song song với bc và đường thẳng qua c song song với ba cắt nhau tại j. chứng minh cfj là tam giác cân. từ đó, so sánh bc và efc/ tia phân giác ngoài của góc a của tam giác abc cắt đường thẳng bc tại i. Gọi n là điểm thuộc bi sao cho bnab. chứng minh: niac
Đọc tiếp
Cho tam gác abc có góc a=75 độ, góc c=35 độ, m là trung điểm của bc. đường thẳng đi qua m và vuông góc với phân giác của góc a cắt ab, ac lần lượt tại e và f
a/ chứng minh rằng: be=cf
b/ đường thẳng qua e song song với bc và đường thẳng qua c song song với ba cắt nhau tại j. chứng minh cfj là tam giác cân. từ đó, so sánh bc và ef
c/ tia phân giác ngoài của góc a của tam giác abc cắt đường thẳng bc tại i. Gọi n là điểm thuộc bi sao cho bn=ab. chứng minh: ni=ac
cho tam giác ABC các đường phân giác cắt nhau ở I. Qua I vẽ đường thẳng song song với BC cắt AB, AC lần lượt ở E, F. Chứng minh EF= BE+CF
cho tam giác đều ABC ,M nằm trong tam giác đó.Qua M kẻ đường thẳng song song với AC và cắt BC tại D, kẻ đường thẳng song song với AB cắt AC tại E,kẻ đường thẳng song song vớiBC cắt AB ở F. gọi h là trung điểm của ef . cm:a) ae=mf b)3 điểm a;i;m thẳng hàng
Cho tam giác đầu ABC. Điểm M nằm giữa B và C. Đường thẳng kẻ qua M và song song với AC cắt AB ở P, đường thẳng kẻ qua M và song song với AB cắt AC ở N.a) Chứng minh tam giác BPM là tam giác đềub) Gọi I là giao điểm của AM và PN, gọi O là trọng tâm của tam giác ABC. Chứng minh rằng tam giác OAN tam giác OBPc)Gọi H là 1 điểm trên đường thẳng BC sao cho HP HN. Chứng minh rằng 3 điểm H,I,O thẳng hàng
Đọc tiếp
Cho tam giác đầu ABC. Điểm M nằm giữa B và C. Đường thẳng kẻ qua M và song song với AC cắt AB ở P, đường thẳng kẻ qua M và song song với AB cắt AC ở N.
a) Chứng minh tam giác BPM là tam giác đều
b) Gọi I là giao điểm của AM và PN, gọi O là trọng tâm của tam giác ABC. Chứng minh rằng tam giác OAN = tam giác OBP
c)Gọi H là 1 điểm trên đường thẳng BC sao cho HP = HN. Chứng minh rằng 3 điểm H,I,O thẳng hàng
Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm E. Trên tia đối của tia CA lấy điểm F sao cho BE=CF. Nối EF cắt BC tại O . Kẻ EI song song với AF ( I thuộc BC)
A CHứng minh tam giác BEI là tam giác cân
B CHứng tỏ OE=OF
C Đường thẳng qua B Và vuông góc với BA cắt đường thẳng qua C và vuông góc với AC tại K. Chứng tỏ tam giác EKF là tam giác cân và OK vuông góc với EF
cho tam giác abc, lấy điểm d thuộc cạnh bc. Qua d kẻ các đường thẳng song song với ab và ac cắt ab và ac theo thừ tự ở e và f.Gọi I là giao điểm của ad và ef
a) Chứng minh tam giác IAE =tam giác IDF
b)Khi d là trung điểm của bc.Chứng minh ef song song với bc









