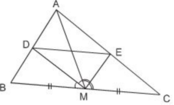
Hình bạn tự vẽ nha.
a, \(\Delta ABC\) có: AM là đường trung tuyến của \(\Delta ABC\)\(\Rightarrow BM=MC\), \(AI=\frac{2}{3}AM\)
\(\Delta AMB\)có: MD là phân giác của \(\widehat{AMB}\)\(\Rightarrow\frac{AD}{DB}=\frac{AM}{MB}\)(tính chất đường phân giác trong tam giác) (1)
\(\Delta AMC\)có: ME là phân giác của \(\widehat{AMC}\)\(\Rightarrow\frac{AE}{EC}=\frac{AM}{MC}\)(tính chất đường phân giác trong tam giác) (2)
Từ (1), (2) và \(BM=MC\left(cmt\right)\Rightarrow\frac{AD}{DB}=\frac{AE}{EC}\)
\(\Delta ABC\)có: \(\frac{AD}{DB}=\frac{AE}{EC}\left(cmt\right)\Rightarrow DE//BC\)(định lý Ta-lét đảo)
b, \(\Delta ABM\)có: \(DI//BM\left(cmt\right)\Rightarrow\frac{DI}{BM}=\frac{AI}{AM}\)(hệ quả của định lý Ta-lét) (3)
\(\Delta AMC\)có: \(IE//MC\left(cmt\right)\Rightarrow\frac{IE}{CM}=\frac{AI}{AM}\)(hệ quả của định lý Ta-lét) (4)
Từ (3), (4) và \(BM=MC\left(cmt\right)\Rightarrow DI=IE\)
c, Ta có: \(\frac{IE}{CM}=\frac{AI}{AM}\left(cmt\right)\)\(\Leftrightarrow\frac{IE}{15}=\frac{\frac{2}{3}AM}{AM}\)\(\Leftrightarrow\frac{IE}{15}=\frac{\frac{2}{3}.10}{10}\)\(\Leftrightarrow\frac{IE}{15}=\frac{2}{3}\)\(\Leftrightarrow IE=10\left(cm\right)\)