Question

Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Gọi O là một điểm bất kỳ nằm trong tam giác ABC. Vẽ điểm M đối xứng với O qua D. Vẽ điểm N đối xứng với O qua E. Chứng minh rằng MNCB là hình bình hành.

Answer 1

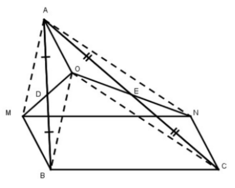
* Xét tứ giác AOBM, ta có:

DA = DB (gt)

DO = DM (định nghĩa đối xứng tâm)

Suy ra: Tứ giác AOBM là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)

⇒ BM // AO và BM = AO (1)

* Xét tứ giác AOCN, ta có: EA = EC (gt)

EO = EN (định nghĩa đối xứng tâm)

Suy ra: Tứ giác AOCN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)

⇒ CN // AO và CN = AO (2)

Từ (1) và (2) suy ra:BM // CN và BM = CN.

Vậy tứ giác BMNC là hình bình hành (vì có 1 cặp cạnh đối song song và bằng nhau).