Các câu hỏi tương tự
Tam giác ABC có ba đường cao AD, BE, CF đồng quy tại H.Chứng minh rằng:AH.DH = BH.EH = CH.FH
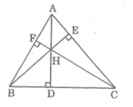
Cho tam giác ABC, các đường cao AD, BE và CF. Gọi H là trực tâm của tam giác.chứng minh:AH.DH=BH.EH=CH.FH
Cho tam giác ABC, các đường cao AD, BE và CF. Gọi H là trực tâm của tam giác.chứng minh:AH.DH=BH.EH=CH.FH
Cho tam giác nhọn ABC có ba đường cao AD, BE, CFcắt nhau tại H. CMR
a, tam giác AEB đồng dạng tam giác AFC
b, tam giác ABC đồng dạng tam giác AEF
c, HD/AD + HE/BE + HF/CF =1
Giúp mk vs !
cho tam giác ABC nhọn, 3 đường cao AD,BE,CF cắt nhau tại H
a) chứng minh : tam giác ABD đồng dạng với tam giác CBF
b) Chứng minh: BH.HE=CH.FH
c) Đường thẳng ED cắt đường thẳng BC tại K. Chứng minh : BK.CD = BD.CE
Cho tam giác ABC nhọn có ba dường cao AD, BE, CF đồng quy tại H. M,N,P lần lượt là các điểm đối xứng của H qua BC, AC và AB. Tính AM / AD + BN / BE + CP / CF
Cho tam giác nhọn ABC có ba đường cao AD, BE, CF đồng quy tai H. M, N, P lần lượt là các điểm đối xứng của H qua BC, AC và AB . TÍnh AM/AD + BN/BE + CP/CF
Cho tam giác ABC nhọn có 3 đường cao AD,BE,CF đồng quy tại H. M,N,P lần lượt là các điểm đối xứng của H qua BC,AC và AB.Tính AM/AD+BN/BE+CP/CF
Cho tam giác ABC nhọn, đường cao AD, BE, CF đồng quy tại H. Chứng minh AE.HC=AH.ED









