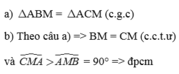Các câu hỏi tương tự
Cho tam giác ABC. Trên tia đối của tia AB và AC lân lượt lấy các điểm C’ và B’ sao cho AB = AB’ và AC = AC’. Gọi M, M’ tương ứng là trung điểm của BC và B’C’. Chứng minh:
a/ BC = B’C’ b/ BC//B’C’ c) AM = AM’ d*/ A, M, M’ thẳng hàng
cho tam giác abc có AB=AC,gọi AM là tia phân giác của góc A(M thuộc BC)
a Chứng minh tam giác AMB = tam giác AMC
b Chứng minh M là trung điểm của cạnh BC và AM ⊥ BC
c Trên tia AM lấy điểm K sao cho MA = MK. Chứng minh AB = CK và AB // CK
cho tam giác ABC có AB = AC, phân giác AM (M thuộc BC)
chứng minh :
a) tam giác AMB= tam giác ACM
b) M là trung điểm của BC và AM vuông góc BC
Bài 1: Cho tam giac ABC, M là trung điểm cua AB. Đường thẳng qua M và song song với BC cắt AC ở I và song song với AB cắt BC ở k. Chứng minh rằng: a) AMIK b) Tam giác AMI bằng tam giác IKC c) AIIC Bài 2: Cho tam giác ABC vuông tại A. Gọi I là trung điểm BC. Trên tia đối của tia IA lấy điểm D sao cho IDIA a) CMR tam giác BID bằng tam giác CIA b) CMR : BD vuông góc với AB c) Qua A kẻ đường thẳng song song với BC cắt đường thẳng BD tại M. C/M tam giác BAM bằng tam giác ABC d) CMR: AB là tia phân gi...
Đọc tiếp
Bài 1: Cho tam giac ABC, M là trung điểm cua AB. Đường thẳng qua M và song song với BC cắt AC ở I và song song với AB cắt BC ở k. Chứng minh rằng: a) AM=IK b) Tam giác AMI bằng tam giác IKC c) AI=IC Bài 2: Cho tam giác ABC vuông tại A. Gọi I là trung điểm BC. Trên tia đối của tia IA lấy điểm D sao cho ID=IA a) CMR tam giác BID bằng tam giác CIA b) CMR : BD vuông góc với AB c) Qua A kẻ đường thẳng song song với BC cắt đường thẳng BD tại M. C/M tam giác BAM bằng tam giác ABC d) CMR: AB là tia phân giác cuả góc DAM Bài 3: Cho tam giác ABC vuông ở A và AB=AC.Gọi K là trung điểm của BC a) C/M: tam giác AKB bằng tam giác AKC b) C/M: AK vuông góc với BC c) từ C vẽ đường vuông góc với BC cắt đường thẳng AB tại E.C/M EK song song với AK Bài 4: Cho tam giác ABC có AB=AC, kẻ BD vuông góc với AC, CE vuông góc với AB(D thuộc AC, E thuộc AB). Gọi O là giao điểm của BD và CE. CMR a) BD= CE b) tam giác OEB bằng tam giác ODC c) AO là tia phân giác cua góc BAC
Cho tam giác ABC có góc B=C. Tia phân giác góc A cắt BC tại D.
Chứng minh:a)AD vuông góc BC
b) Gọi M;N lần lượt là trung điểm AB và AC. C/M góc BMD=CND
c)C/M MN vuông góc AD và MN//BC
BÀI 1: Cho tam giác ABC có ABAC.Tia phân giác của BÂC cắt BC tại điểm M.a/Chứng minh rằng hình tam giác AMb tam giác AMC và M là trung điểm của BC.b/Tính góc AMB.c/Vẽ ME // AB(E thuộc AC).Chứng minh rằng:góc EMCgóc ECMd/Trên canh AB lấy điểm K sao cho AK AE.Chứng minh rằng :KE//BCBÀI 2:Cho tam giác ABC vuông tại A có M là trung điểm của BCa)Tính góc B +góc Cb)Chọn điểm D sao cho M là trung điểm của AD.Chứng minh :tam giác AMB tam giác DMCc)Chứng minh ACvuoong góc CDd)Chứng minh :AM1/2BC
Đọc tiếp
BÀI 1: Cho tam giác ABC có AB=AC.Tia phân giác của BÂC cắt BC tại điểm M.
a/Chứng minh rằng hình tam giác AMb= tam giác AMC và M là trung điểm của BC.
b/Tính góc AMB.
c/Vẽ ME // AB(E thuộc AC).Chứng minh rằng:góc EMC=góc ECM
d/Trên canh AB lấy điểm K sao cho AK =AE.Chứng minh rằng :KE//BC
BÀI 2:Cho tam giác ABC vuông tại A có M là trung điểm của BC
a)Tính góc B +góc C
b)Chọn điểm D sao cho M là trung điểm của AD.Chứng minh :tam giác AMB= tam giác DMC
c)Chứng minh ACvuoong góc CD
d)Chứng minh :AM=1/2BC
Bài 9: Cho tam giác ABC có :AB= AC; M là trung điểm của BC.
a) AM là phân giác của góc BAC và AM vuông góc BC.
b) Qua C kẻ đường thẳng song song với AB cắt AM tại D. Chứng minh rằng: M là trung điểm của AD.
c) Qua B kẻ đường thẳng vuông góc AC và cắt AC tại H. Tính số đo góc HBD ?
GT: tam giác ABC, AB=AC,phân giác AM (M thuộc BC)
LK: a, c/m tam giác ABC=tam giác ACM
b, c/m M là trung điểm BC và AM vuông góc BC
: Cho tam giác ABC có AB = AC, gọi AM là tia phân giác của góc A(M thuộc BC). a) Chứng minh tam giác AMB = tam giác AMC
b) Chứng minh M là trung điểm của cạnh BC và AM ⊥ BC.
c) Trên tia AM lấy điểm K sao cho MA = MK. Chứng minh AB = CK và AB // CK