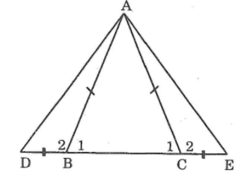
*) Ta có: ΔABC cân tại A

BD = CE (giả thiết)
Suy ra: ΔABD = ΔACE (c.g.c)
⇒ AD = AE ( hai cạnh tương ứng)
*) Tam giác ADE có AD = AE nên tam giác này cân tại A (theo định nghĩa tam giác cân)

*) Ta có: ΔABC cân tại A

BD = CE (giả thiết)
Suy ra: ΔABD = ΔACE (c.g.c)
⇒ AD = AE ( hai cạnh tương ứng)
*) Tam giác ADE có AD = AE nên tam giác này cân tại A (theo định nghĩa tam giác cân)
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh rằng ∆ADE là tam giác cân.
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE, Chứng minh tam giác ADE cân.
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE. Chứng minh tam giác ADE là tam giác cân
CHO TAM GIAC ABC CÂN TẠI A. TRÊN TIA ĐỐI CỦA BC LẤY ĐIỂM D, TRÊN TIA ĐỐI CÚA CB LẤY ĐIỂM E SAO CHO BD=CE. CHỨNG MINH TAM GIÁC ADE LÀ TAM GIÁC CÂN
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE. Chứng minh:
a) Tam giác ADE cân
b) Tam giác ABD = tam giác ACE
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy M, trên tia đối của CB lấy N sao cho BM = BN. Vẽ BD vuông góc với AM tại D, CE vuông góc với AN tại E.
a) Chứng minh rằng tam giác AMN cân.
b) Chứng minh rằng BD = CE.
c) Gọi K là giao điểm của DB và EC. Chứng minh tam giác ADK = tam giác AEK.
d) Chứng minh rằng KD + KE < 2KA.
cho tam giác abc cân tại A. Trên tia đối của tia bc lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE. Chứng minh tam giác ADE là tam giác cân GIÚP MÌNH VỚI MÌNH ĐANG CẦN GẤP
cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D sao cho AB = BD. Trên tia đối của tia CB lấy điểm E sao cho AC = CE. Chứng minh DE = AB+AC+BC
cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D sao cho AB = BD. Trên tia đối của tia CB lấy điểm E sao cho AC = CE. Chứng minh DE = AB+AC+BC