Chọn C.
+ Tính góc A
Áp dụng định lí cosin trong tam giác ta có:
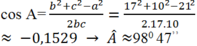
+Tính góc B:
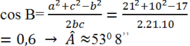
Chọn C.
+ Tính góc A
Áp dụng định lí cosin trong tam giác ta có:
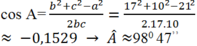
+Tính góc B:
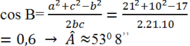
Cho tam giác ABC, biết a = 21cm, b = 17cm, c = 10cm. Tính độ dài đường trung tuyến ma
A. 7,32
B. 8,46
C. 8,94
D. 9,18
Tam giác ABC biết A (2;-1) và phương trình hai đường phân giác trong của góc B và góc C lần lượt là d: x - 2y + 1=0, d2 : 2x - 3y + 6 = 0 . Xác định tọa độ B, C.
Cho tam giác ABC, biết A(2;−1) và 2 phân giác trong của góc B, C lần lượt là: x−2y+1=0; 2x - 3y + 6=0. Hãy lập phương trình các cạnh của tam giác trên.
Cho tam giác ABC có A(2;−1). Đường phân giác trong góc B và C có phương trình lần
lượt là d1 :x−2y+1=0 và d2 :x+y+3=0. Viết phương trình đường thẳng chứa các cạnh của tam giác ABC.
Tam giác ABC có các cạnh a = 8cm, b = 10cm và c = 13cm.
a) Tam giác đó có góc tù không?
b) Tính độ dài trung tuyến MA của tam giác ABC đó.
Cho tam giác ABC. Gọi H là trực tâm của tam giác ABC và A' ; B' ; C' lần lượt là chân đường vuông góc hà từ A, B, C lên các cạnh BC, AC, AB. Chứng minh rằng \(B'C'.\overrightarrow{HA'}+C'A'.\overrightarrow{HB'}+A'B'.\overrightarrow{HC'}=\overrightarrow{0}\)
Cho tam giác abc cân tại a.d là trung điểm ac.k(1;0);e(1/3;4) lần lượt là tâm đường tròn ngoại tiếp tam giác abc và trọng tâm tam giác abd.p(-1;6);q(-9;2) lần lượt thộc ac,bd.tìm tọa độ a,b,c biết hoành độ của d :xd>0
Cho tam giác ABC có a,b,c,ma,mb,mc,R lần lượt là độ dài các cạnh BC,CA,AB, độ dài các đường trung tuyến kẻ từ A,B,C và bán kính đường tròn ngoại tiếp tam giác. Biết rằng: \(\frac{a^2+b^2}{mc}+\frac{b^2+c^2}{ma}+\frac{c^2+a^2}{mb}=12R\). Chứng minh rằng tam giác ABC đều
Cho tam giác ABC có A(2; -1) và các đường phân giác trong góc B và C lần lượt
có phương trình: x - 2y + 1= 0 ; x + y + 3 = 0.
Lập phương trình đường thẳng BC.