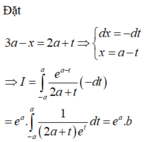Các câu hỏi tương tự
nếu 0<a<b<c<d<e<f
(a-b)(c-d)(e-f).x=(b-a)(d-c)(f-e) thì x=...
Cho hàm số đa thức bậc ba y f (x) có đồ thị đi qua các điểm A(2;4), B(3;9), C(4;16). Các đường thẳng AB, AC, BC lại cắt đồ thị tại lần lượt tại các điểm D, E, F (D khác A và B, E khác A và C, F khác B và C). Biết rằng tổng các hoành độ của D, E, F bằng 24. Tính f(0) A.
π
4
B. 0 C.
24
5
D. 2
Đọc tiếp
Cho hàm số đa thức bậc ba y = f (x) có đồ thị đi qua các điểm A(2;4), B(3;9), C(4;16). Các đường thẳng AB, AC, BC lại cắt đồ thị tại lần lượt tại các điểm D, E, F (D khác A và B, E khác A và C, F khác B và C). Biết rằng tổng các hoành độ của D, E, F bằng 24. Tính f(0)
A. π 4
B. 0
C. 24 5
D. 2
Biết rằng phương trình
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
e
0
a
,
b
,
d
,
e
∈
ℝ
,...
Đọc tiếp
Biết rằng phương trình a x 4 + b x 3 + c x 2 + d x + e = 0 a , b , d , e ∈ ℝ , a ≠ 0 , b ≠ 0 có 4 nghiệm thực phân biệt. Hỏi phương trình sau có bao nhiêu nghiệm thực?
4
a
x
3
+
3
b
x
2
+
2
c
x
+
d
2
−
2
6
a
x
2
+
3
b
x
+
c
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
e
=
0
A. 0
B. 2
C. 4
D. 6
Cho hàm số
f
(
x
)
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
e
,
(
a
,
b
,
c
,
d
,
e
∈
ℝ
)
Hàm yf(x) có bảng xét dấu như sau: Số nghiệm của phương trình f(x)e là A....
Đọc tiếp
Cho hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e , ( a , b , c , d , e ∈ ℝ ) Hàm y=f'(x) có bảng xét dấu như sau:
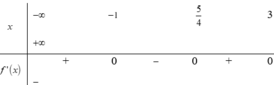
Số nghiệm của phương trình f(x)=e là
A. 1
B. 0
C. 2
D. 3
Cho hàm số đa thức bậc ba y f(x) có đồ thị đi qua các điểm
A
2
;
4
,
B
3
;
9
,
C
4
;
16
. Các đường thẳng AB, AC, BC lại cắt đồ thị tại lần lượt tại các điểm D, E, F (D khác A và B; E khác A và C; F khác B và C). Biết rằng tổng các hoành độ của D, E, F bằng 24. Tính ...
Đọc tiếp
Cho hàm số đa thức bậc ba y = f(x) có đồ thị đi qua các điểm A 2 ; 4 , B 3 ; 9 , C 4 ; 16 . Các đường thẳng AB, AC, BC lại cắt đồ thị tại lần lượt tại các điểm D, E, F (D khác A và B; E khác A và C; F khác B và C). Biết rằng tổng các hoành độ của D, E, F bằng 24. Tính f 0
A. -2
B. 0
C. 24 5
D. 2
Tìm A, B, C, D, E biết : ABCD x E = DCBA
Cho tam giác ABC có 2 x góc A = 3 x góc B = 6 x góc C
a. tính số đo các góc A, B ,C
b. gọi M là trung điểm của BC , qua M kẻ MY / AC cắt AB tại D VÀ MX // AB cắt AC tại E . Chứng minh tam giác BMD = tg MGE
Cho các mệnh đề sau:(I). Nếu
a
b
c
t
h
ì
2
ln
a
ln
b
+
ln
c
(II). Cho số thực 0 a ≠ 1. Khi đó
a
-
1
log
a
x
≥
0...
Đọc tiếp
Cho các mệnh đề sau:
(I). Nếu a = b c t h ì 2 ln a = ln b + ln c
(II). Cho số thực 0 < a ≠ 1. Khi đó a - 1 log a x ≥ 0 ⇔ x ≥ 1
(III). Cho các số thực 0 < a ≠ 1 , b > 0 , c > 0 . Khi đó b log a c ≥ 0 ⇔ x ≥ 1
(IV). l i m x → + ∞ 1 2 x = - ∞ .
Số mệnh đề đúng trong các mệnh đề trên là
A. 3
B. 4
C. 2
D. 1
Cho hàm số f(x) liên tục trên (1;e) thỏa mãn
x
f
x
−
f
1
+
ln
x
x
2
+
x
−
2
−
ln
x
. Biết rằng
∫
2
e
f
x
d
x
a
e...
Đọc tiếp
Cho hàm số f(x) liên tục trên (1;e) thỏa mãn x f x − f 1 + ln x = x 2 + x − 2 − ln x . Biết rằng ∫ 2 e f x d x = a e 2 + b e + c với a , b , c ∈ Q . Tính giá trị của T = a + b + c.
A. T = 11 2 .
B. T = -4
C. T = − 5 2 .
D. T = 3