Các câu hỏi tương tự
Cho A; B; C tương ứng là các điểm trong mặt phẳng phức biểu diễn các số phức z1 1 + 2i; z2 -2 + 5i ; z3 2 + 4i . Số phức z biểu diễn bởi điểm D sao cho tứ giác ABCD là hình bình hành là A. -1 + 7i. B. 5 + i. C. 1 + 5i. D. 3 + 5i.
Đọc tiếp
Cho A; B; C tương ứng là các điểm trong mặt phẳng phức biểu diễn các số phức z1 = 1 + 2i; z2 = -2 + 5i ; z3 = 2 + 4i . Số phức z biểu diễn bởi điểm D sao cho tứ giác ABCD là hình bình hành là
A. -1 + 7i.
B. 5 + i.
C. 1 + 5i.
D. 3 + 5i.
Trong mặt phẳng với hệ toạ độ Oxy cho điểm A(4; 4) và M là điểm biển diễn số phức z thoả mãn điều kiện
z
-
1
z
+
2
-
i
. Tìm toạ độ điểm M để đoạn thẳng AM nhỏ nhất. A. M (-1; -1) B. M (-2; -4) C. M ( 1; 5) D. M (2; 8)
Đọc tiếp
Trong mặt phẳng với hệ toạ độ Oxy cho điểm A(4; 4) và M là điểm biển diễn số phức z thoả mãn điều kiện z - 1 = z + 2 - i . Tìm toạ độ điểm M để đoạn thẳng AM nhỏ nhất.
A. M (-1; -1)
B. M (-2; -4)
C. M ( 1; 5)
D. M (2; 8)
Điểm M biểu diễn số phức z=3+2i trong mặt phẳng tọa độ phức là
A. M(2;3)
B. M(-3;-2)
C.M(3;2)
D. M(3;-2)
Điểm M biểu diễn số phức z = 3 + 2 i trong mặt phẳng tọa độ phức là:
A. M(2; 3)
B. M(3; 2)
C. M(3;-2)
D. M(-3;-2)
Trong mặt phẳng tọa độ Oxy, cho điểm M là điểm biểu diễn của số phức z=4+2i.
Phương trình đường trung trực của đoạn OM là:
A. x+2y+5=0
B. x+2y-5=0
C. x-2y+5=0
D. 2x+y+5=0
Trong mặt phẳng tọa độ Oxy, gọi M là điểm biểu diễn số phức
z
1
-
2
i
, N là điểm biểu diễn số phức
z
¯
1
-
i
2
z
. Tính diện tích tam giác OMM′.
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, gọi M là điểm biểu diễn số phức z = 1 - 2 i , N là điểm biểu diễn số phức z ' ¯ = 1 - i 2 z . Tính diện tích tam giác OMM′.
![]()
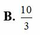
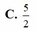
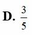
Cho số phức
z
(
2
-
3
i
)
(
4
-
i
)
3
+
2
i
. Tìm tọa độ điểm biểu diễn của số phức z trên mặt phẳng Oxy A. . B. . C. . D. .
Đọc tiếp
Cho số phức z = ( 2 - 3 i ) ( 4 - i ) 3 + 2 i . Tìm tọa độ điểm biểu diễn của số phức z trên mặt phẳng Oxy
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Trong mặt phẳng phức Oxy, các số phức z thỏa mãn
z
+
2
i
-
1
z
+
i
. Mô dul của số phức z được biểu diễn bởi điểm M sao cho MA ngắn nhất với A(1;3) là A.
10
B.
7
C.
2...
Đọc tiếp
Trong mặt phẳng phức Oxy, các số phức z thỏa mãn z + 2 i - 1 = z + i . Mô dul của số phức z được biểu diễn bởi điểm M sao cho MA ngắn nhất với A(1;3) là
A. 10
B. 7
C. 2 3
D. 2 5
Trong mặt phẳng Oxy, gọi M là điểm biểu diễn của số phức z3-4i và M là điểm biểu diễn của số phức . Diện tích của tam giác OMM bằng A.25/4 B.25/2 C.15/4 D.15/2
Đọc tiếp
Trong mặt phẳng Oxy, gọi M là điểm biểu diễn của số phức z=3-4i và M' là điểm biểu diễn của số phức ![]() . Diện tích của tam giác OMM' bằng
. Diện tích của tam giác OMM' bằng
A.25/4
B.25/2
C.15/4
D.15/2



