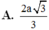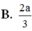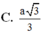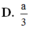Đáp án B
Các cạnh bên bằng nhau ⇒ S O ⊥ ( A B C D )
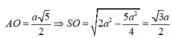
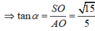
Đáp án B
Các cạnh bên bằng nhau ⇒ S O ⊥ ( A B C D )
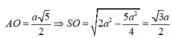
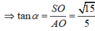
Cho S.ABCD,ABCD là hình chữ nhật có AB = 2a; AD = 2a. Các cạnh bên bằng nhau và bằng a 2 . Góc tạo bởi giữa cạnh bên và đáy bằng a. Khi đó a = ?
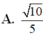
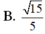
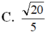
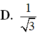
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, A D = 2 a , cạnh bên SA vuông góc với đáy và SA = 2a. Gọi M, N lần lượt là trung điểm của cạnh SA, CD và α là góc giữa đường thẳng MN và mặt phẳng (SBD). Khi đó sin α bằng
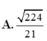
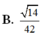
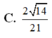
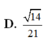
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a, AD=2a, SA=2a và SA ⊥ (ABCD), Gọi a là góc giữa 2 đường thẳng SC và BD. Khi đó, cos α bằng
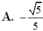
![]()
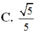
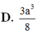
Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông góc với mặt đáy (ABCD), AB = a, AD = 2a. Góc giữa cạnh bên SB và mặt phẳng (ABCD) bằng 45 ° . Thể tích hình chóp S.ABCD bằng
A. 2 a 3 3
B. a 3 3
C. 6 a 3 18
D. 2 2 a 3 3
Cho hình chóp S.ABCD có các cạnh bên bằng nhau và bằng 2a, đáy là hình chữ nhật ABCD có AB=2a, AD=a. Gọi K là điểm thuộc BC sao cho 2 B K → + 2 C K → = 0 → . Tính khoảng cách giữa hai đường thẳng AD và SK.
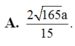
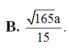
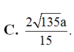
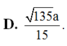
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=1, AD=2 cạnh bên SA vuông góc với đáy và S A = 5 . α là số đo góc giữa hai mặt phẳng (SAB) và (SBD), cos α = ?
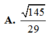
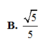
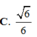
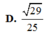
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,AB=a, AD=2a; cạnh bên SA vuông góc với mặt đáy và S A = a 5 . Khoảng cách giữa hai đường thẳng AB và SD bằng
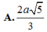
![]()
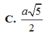
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=a; AD=2a, cạnh bên SA vuông góc với đáy và thể tích khối chóp S.ABCD bằng 2 a 3 3 . Tính số đo góc giữa đường thẳng SB với mặt phẳng (ABCD).
A. 30 0
B. 60 0
C. 45 0
D. 75 0
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB=a, AD=2a; SA vuông góc với đáy ABCD, SC hợp với đáy một góc α và tan α . Khi đó, khoảng cách từ điểm B đến mặt phẳng (SCD) là: