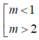PT có 2 nghiệm phân biệt
\(\Leftrightarrow\text{Δ}>0\Leftrightarrow\left(2m\right)^2-4.\left(m+1\right)\left(m-1\right)>0\)
\(\Leftrightarrow4m^2-4\left(m^2-1\right)>0\Leftrightarrow4>0\)(luôn đúng)
Vậy PT luôn có 2 nghiệm phân biệt
Theo hệ thức Viét ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{2m}{m+1}\\x_1.x_2=\dfrac{m-1}{m+1}\end{matrix}\right.\)
Mà theo GT thì ta có:
\(x_1^2+x_2^2=5\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1.x_2=5\)
\(\Leftrightarrow\left(\dfrac{-2m}{m+1}\right)^2-2.\dfrac{m-1}{m+1}=5\)
\(\Leftrightarrow\dfrac{4m^2}{\left(m+1\right)^2}-\dfrac{2\left(m-1\right)}{m+1}=5\)
\(\Leftrightarrow\dfrac{1}{m+1}\left[\dfrac{4m^2}{m+1}-2\left(m-1\right)\right]=5\)
\(\Leftrightarrow\dfrac{2m^2+2}{m^2+2m+1}=5\)
\(\Leftrightarrow2m^2+2=5m^2+10m+5\)
\(\Leftrightarrow3m^2+10m+3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-\dfrac{1}{3}\\m=-3\end{matrix}\right.\)